Excel(エクセル)の統計用の関数の中で、ベータ分布に対して累積分布関数や確率密度関数や逆関数を計算する関数があります。『BETA.DIST(ベータディストリビューション)』・『BETADIST(ベータディストリビューション)』・『BETA.INV(ベータインバース)』・『BETAINV(ベータインバース)』です。ディストリビューションという名前がついている方が、確率密度関数や累積分布関数を計算する関数で、インバースの方が逆関数になります。関数の名前には『.(ドット)』がついている物ついていない物がありますね。Excelのバージョンが新しくなった時に出来たのが『.(ドット)』がついている方です。計算できる内容も若干変わった所がありますので、使い方を確認しましょう。
目次
ベータ分布ってどんな時の分布でしょうか?
簡単にベータ分布の確認だけしておきましょう。
例えばサイコロを振った時に『1から3の間の数値』と『4から5の間の数値』が出る確率を考える事にしましょう。理論上はどっちも50%の確率で出て来る事になります。これを実際に5回降ってみた所、1から3の数値が1回、4から5の数値が4回出て来たとします。この結果だけ見れば、1から3の確率が5分の1、4から5の確率が5分の4という事になりますね。しかし5回くらいであればたまたまそうなってしまったという事も考えられます。なのでこの結果から確率を決定する事は出来ないと思います。ではどんな確率になるかと言うと、『表が出る確率が5分の1くらいだけど、試行回数が少ないので確実には言えない』と言った感じですね。5分の1になるのが有力だけど回数が増えると変わる可能性があるという事ですね。これを分布であらわすと、5分の1の所が一番高いグラフになって、そこから離れるとその確率は徐々に減る様な分布のグラフになりますね。これがベータ分布になります。こういった分布の中で、指定した値が分布のどの位置にあるのか、どのくらいの割合数あるのかを求めるのが今回の関数になります。
Excelの『BETA.DIST』と『BETADIST』でベータ分布を分析してみよう
ではベータ分析の確率密度関数と累積分布関数を計算してみましょう。
ここで使うのは『BETA.DIST』と『BETADIST』です。『BETA.DIST』が新しい方の関数です。『BETADIST』については前からある関数ですが、確率密度関数の計算は出来ませんので気を付けてくださいね。
『BETA.DIST』と『BETADIST』の書き方を確認しておこう!
それぞれについて引数の指示の仕方をチェックしておきましょう!
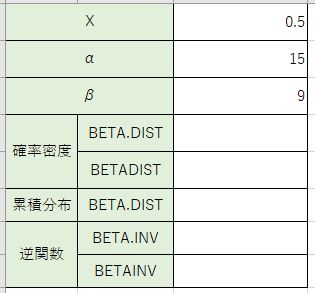
関数式:『=BETA.DIST(x、α、β、関数の種類)』
関数式:『=BETADIST(x、α、β)』
BETA.DISTについては最後に関数の種類を指定してください。『fakse』が確率密度関数の計算で『True』が累積分布関数の計算になります。BETADISTの方は累積分布関数の計算のみなのでそこの指定をする部分は無くてもいいという事になる訳ですね。
『BETA.DIST』と『BETADIST』で確率密度関数と累積分布関数を計算してみよう!
Excelにベータ分布に必要な数値を指定しています。
今回のxが分布の中でどこの位置にあるのか、xの数値が全体のどのくらいの割合なのかを計算する事になります。
確率密度の計算では、『=BETA.DIST(C1、C2、C3、FALSE)』と書き込みましょう。
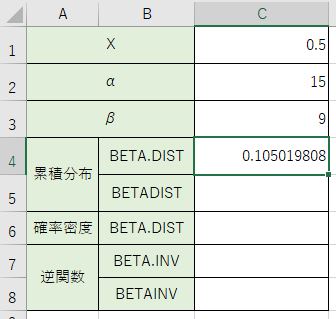
これが分布の左から考えた時のxの位置を表す累積分布の計算結果という事ですね。
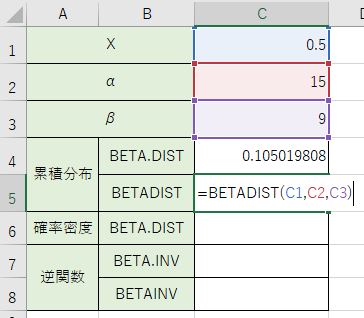
以前の関数での計算では『=BETADIST(C1、C2、C3)』という事になります。
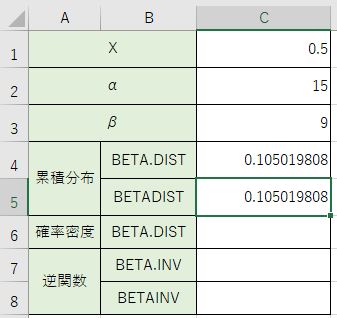
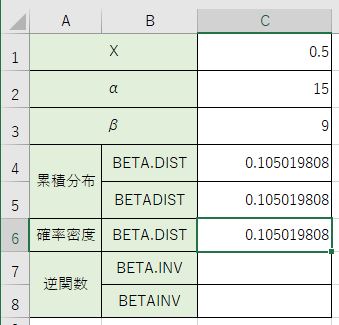
同じ数値で結果が出て来ているのが分かりますね。
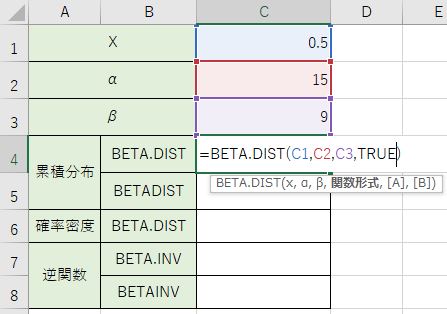
確率密度をやりたい場合は『=BETA.DIST(C1、C2、C3、TRUE)』と書いてくださいね。
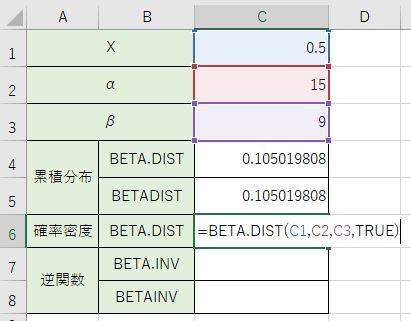
これが分布の中でのXの数値の割合という事になります。
Excelの『BETA.INV』と『BETAINV』で確率から数値を出してみよう
ではベータ分析の逆関数をやってみましょう!
逆関数は累積分布確率からその位置にあたる数値を計算する物になります。xの値という所ですね。
ここで使うのは『BETA.INV』と『BETAINV』です。『BETA.INV』が新しい方の関数ですがこの2つに関しては結果についての違いはありません。
『BETA.INV』と『BETAINV』の書き方を確認しておこう!
それぞれについて引数の指示の仕方をチェックしておきましょう!
関数式:『=BETA.INV(確率、α、β)』
関数式:『=BETADIST(確率、α、β)』
どちらも同じ内容になっていますね。引数にある確率は累積分布確率になります。確率密度の方ではエラーになってしまうので気を付けましょう。
『BETA.INV』と『BETAINV』で逆関数の計算してみよう!
同じExcelにベータ分布に必要な数値を指定しています。
今度はさっきのBETA.DISTで出した累積分布確率の数値からXの値を求めてみましょう。
確率密度の計算では、『=BETA.INV(C4、C2、C3)』と書き込みましょう。
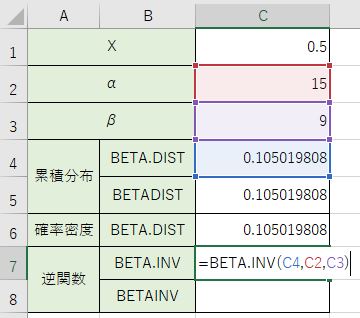
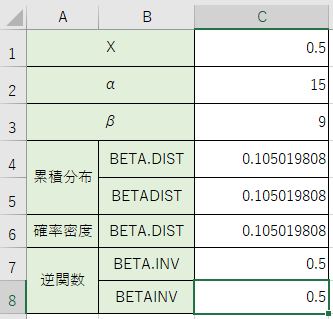
これでC1に書き込んであるXと同じ数値になっているのが分かりますね。これが逆関数です。
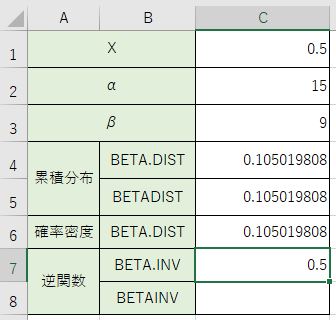
以前の関数での計算では『=BETAINV(C4、C2、C3)』という事になります。
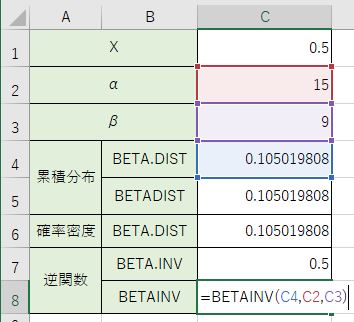
同じ数値で結果が出て来ているのが分かりますね。
Excelでベータ分布の確率密度関数と累積分布関数、逆関数を計算する【BETA.DIST】【BETADIST】【BETA.INV】【BETAINV】関数|【まとめ】
Excelでのベータ分布の分析用の関数として4つ、『BETA.DIST』・『BETADIST』・『BETA.INV』・『BETAINV』の書き方を紹介しました。累積分布なのか確率密度なのか逆関数なのかという事で計算したい内容によって使い分けが大切でしたね。
後は名前に『.』がついているのが新しいやつなので、前のやつはいつ使えなくなるか分からないので新しい方を活用して行きましょうね。
分布に対しての関数はまだありますので別途紹介して行きます。