Excel(エクセル)のでデータの解析、分析をする時の関数の1つの、データの共分散を計算するCOVAR(コバリアンス)関数、COVARIANCE.P(コバリアンス・ピー)関数、、COVARIANCE.S(コバリアンス・エス)関数を紹介します。前回、2つのデータの相関関係、相関係数を計算する関数もやりましたね。この相関係数というのがデータの関係性を表す数字です。
例えば、
- 身長が伸びると体重が増えるという関係性
- 気温が上がるとビールの売り上げが上がる
- テストの合計点が高いと、個々の科目の点数も高い
といった所ですね。データの関係性は統計学でよく使われます。そしてデータ分析が出来る事って大切です。これから夏になるっていう時にストーブが売られないのは、夏には売れないというデータ分析が出来ているからですね。極端な例ではありましたが、売り上げを伸ばす為の戦略を考えたりする事に役立てられるとよいですよね。
今回は、この共分散を求められるCOVAR関数、COVARIANCE.P関数、、COVARIANCE.S関数の使い方を紹介します。関数を使ってデータ分析を出来る様にして行きましょう!
COVAR関数、COVARIANCE.P関数、COVARIANCE.S関数の説明動画はこちら!!↓↓
目次
COVAR関数、COVARIANCE..P関数、COVARIANCE..S関数の書き方
【=COVAR(配列1、配列2)】
【=COVARIANCE.P(配列1、配列2)】
- 2つのデータの関係性を表す共分散を計算する関数です。
- どちらも同じ計算です。どちらを使っても計算結果は同じになります
- COVARIANCE..Pの方が新しいバージョンのExcelで使用できる関数です。
- 計算結果の数字の大きさでデータの関係性を考える事が出来ます。
【=COVARIANCE.P(配列1、配列2)】
- 2つのデータの不偏共分散を計算する関数です。
- 使用する引数の指定は、COVAR・COVARIANCE.Pと同じ指定です。
- 母集団の数値を推定した共分散の値を計算出来ます。
COVAR|COVARIANCE.P|COVARIANCE.Sの3つは、引数の指定の仕方が同じになります。計算内容としてはCOVARIANCE.Sは不偏共分散の計算になり、母集団の値を推測して計算をしてくれます。より正確な値として分析出来そうです。が、あくまで推測しての母集団なので、どこまでを信用して考えるかが大事ですね。
データ分析出来る!共分散の計算をしてみよう!
では、実際に共分散の計算をしてみましょう。共分散の計算結果の数値が大きければ2つのデータに関係性があると言えて、数値が小さければ関係性は低いと言えます。この数値の大きさで関係性を判断していくわけですね。
関数の使い方自体はそれほど難しくなく、引数に比べたい2つのデータを指定するだけになっています。共分散か不偏共分散かによって同じデータを使っても結果は変わります。使い分けられる様に覚えていきましょう!
関係性のなさそうなデータの共分散を計算してみよう!
関係性の低そうなデータの集まりから共分散を計算してみます。【COVAR関数・COVARIANCE.P関数・COVARIANCE.S関数】で計算してみるので、どの様に数値が変わるか確認しましょう!
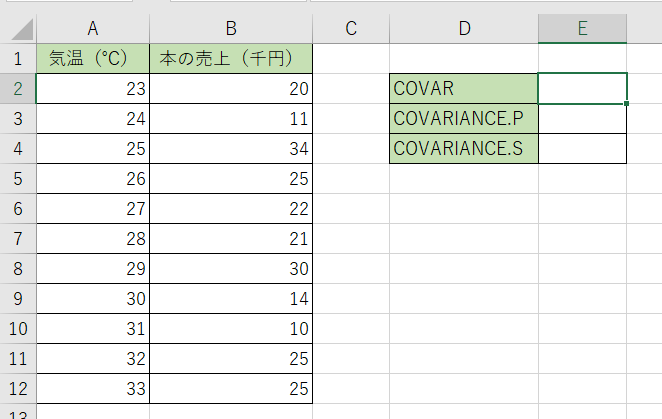
COVAR関数の計算
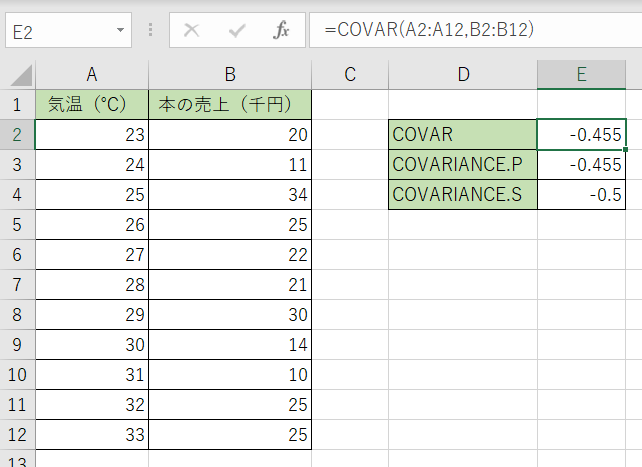
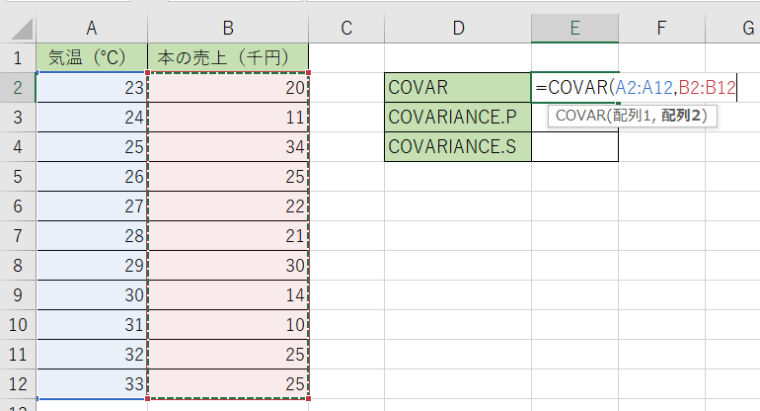
1.計算結果を表示させるセルにCOVAR関数を入力します。
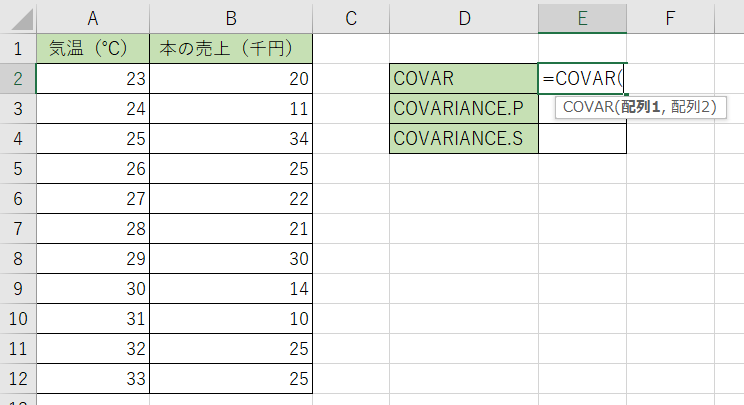
2.1つ目の引数にA列のデータ、2つ目にB列のデータを選択します。
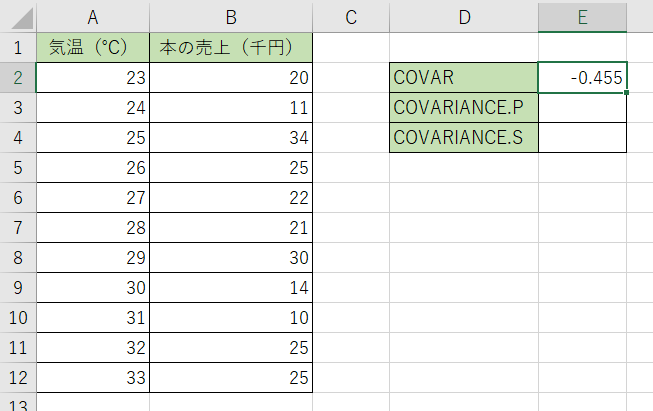
3.決定すると答えが出て来ます。今回の数値は『-0,455』でした。
COVARIANCE.P関数の計算
ではCOVARIANCE.P関数を使用した計算をしてみましょう
1.計算結果を表示させるセルにCOVARIANCE.P関数を入力します。
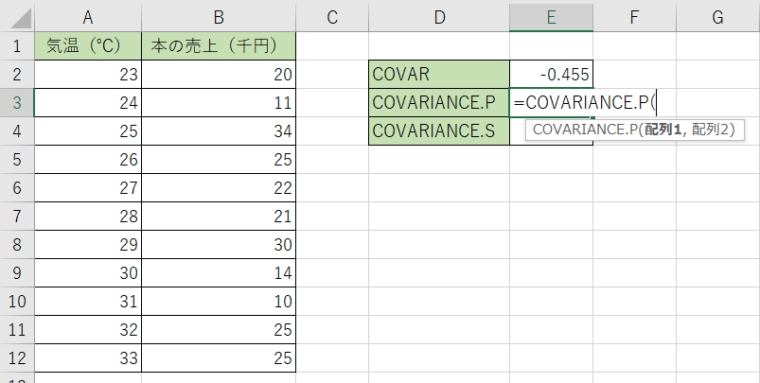
2.1つ目の引数にA列のデータ、2つ目にB列のデータを選択します。
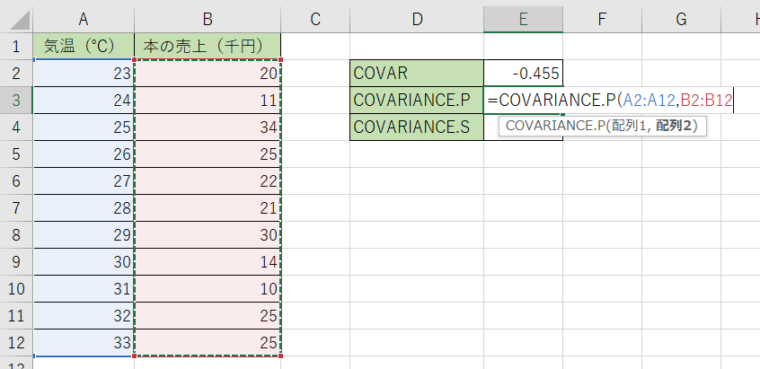
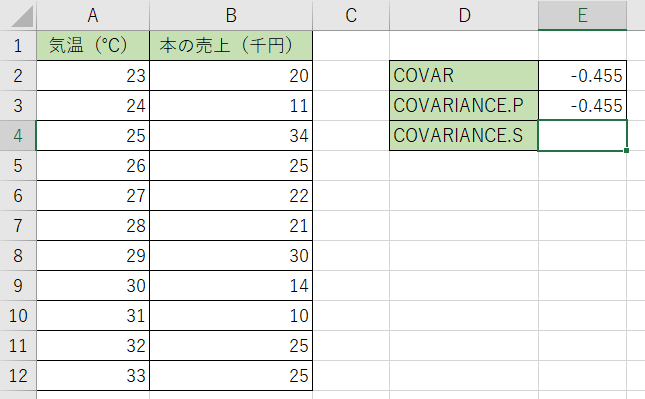
3.関数を決定すると答えが出て来ます。結果が『-0,455』になりましたね。
比べてみると、COVARの時の計算と同じ結果が出ているのが分かりますね。
COVARIANCE.S関数の計算
最後にCOVARIANCE.S関数を使用した計算をしてみましょう
1.同様に計算結果を表示させるセルにCOVARIANCE.S関数を入力します。
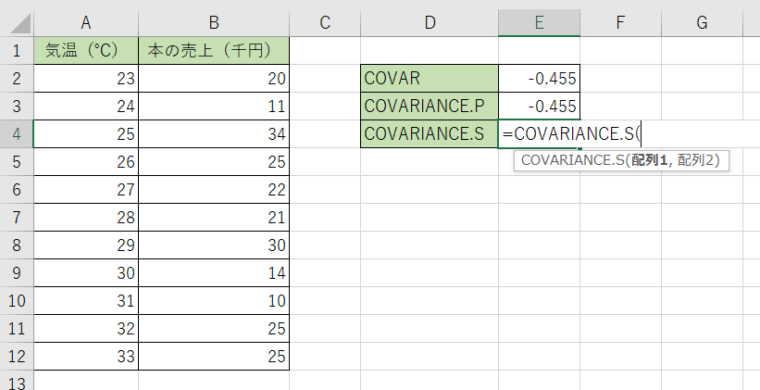
2.引数の指定も同じで、1つ目の引数にA列のデータ、2つ目にB列のデータを選択します。
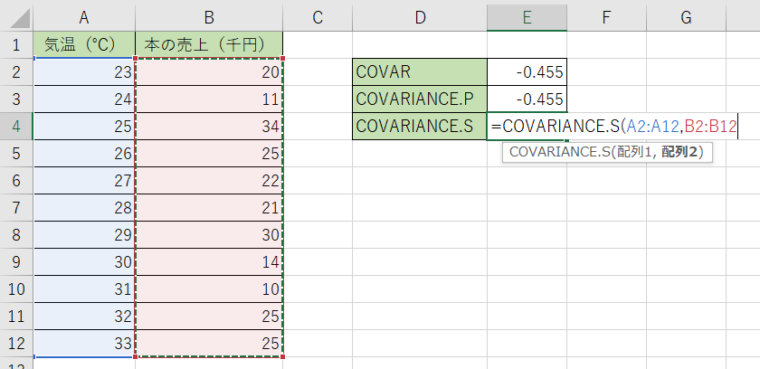
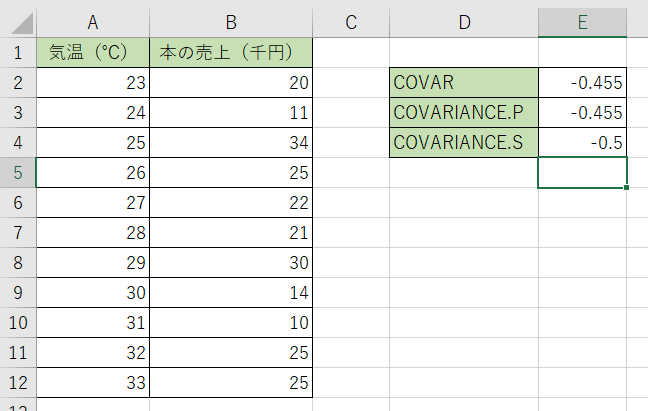
3.関数を決定すると答えが出て来ます。結果が『-0,55』になりましたね。
母数を推定して計算するCOVARIANCE.Sの場合は他の関数と比べると、数値が若干変わります。データ量が多ければさらに差が出てきたりします。どちらの数値で考えるか気を付けて使い分けて下さいね。
関係性の高そうなデータの共分散を計算してみよう!
次は関係性の高そうなデータの集まりから共分散を計算してみます。計算の流れは先ほどと同じようになります。3つの関数で計算するので、結果の違いをチェックしましょう。
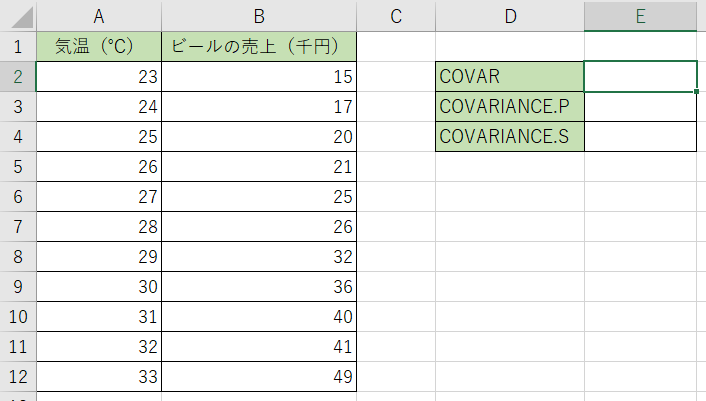
COVAR関数の計算
計算の流れは上記と同じ流れになります。
1.計算結果を表示させるセルにCOVAR関数を入力します。
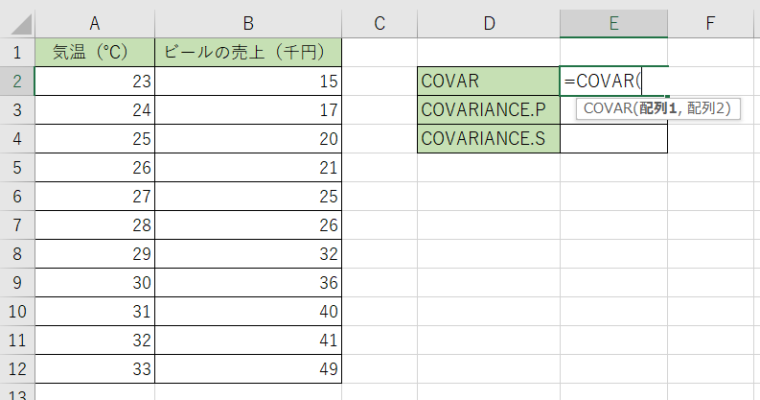
2.1つ目のデータと2つ目のデータを選択します。
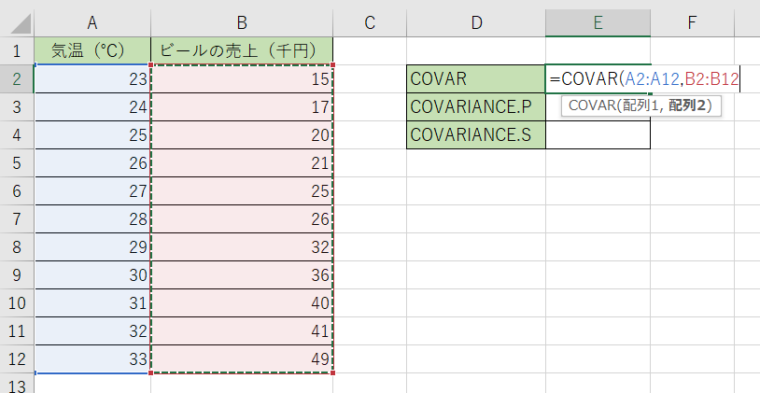
3.関数を決定すると答えが出て来ます。今回は『33』になりました。
数値が大きいので2つのデータに関係性があると言えますね。
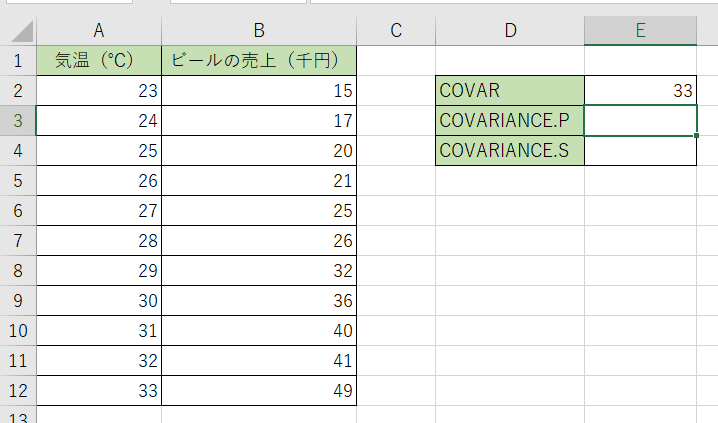
COVARIANCE.P関数の計算
では同じ数値を使ってCOVARIANCE.P関数を使用した計算をしてみましょう
1.同様に計算結果を表示させるセルにCOVARIANCE.Pを入力します。
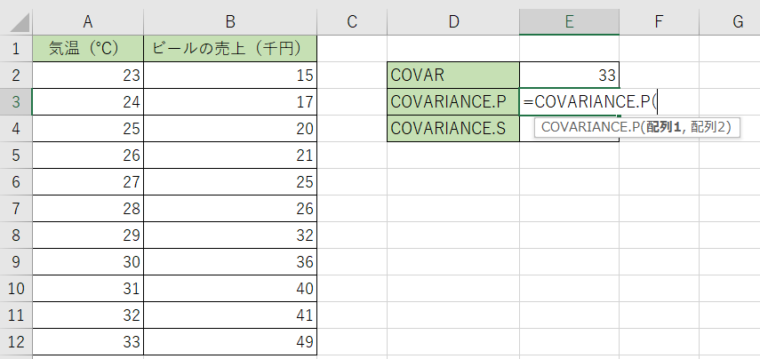
2.引数にA列のデータとB列のデータを選択します。
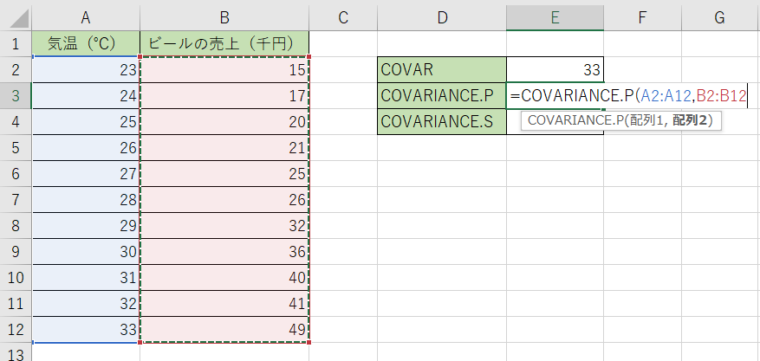
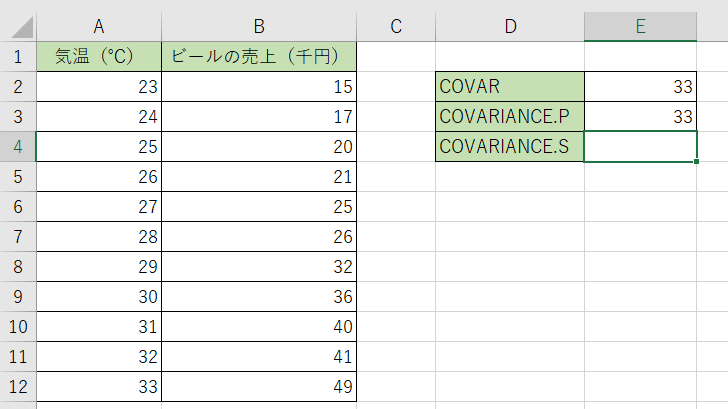
3.関数を決定すると答えが出て来ます。結果が『33』になりましたね。
COVARと同様に計算されているのが確認出来ましたね。
COVARIANCE.S関数の計算
最後にCOVARIANCE.S関数を使用した不偏共分散の計算をしてみましょう
1.計算結果を表示させるセルにCOVARIANCE.Sを入力します。
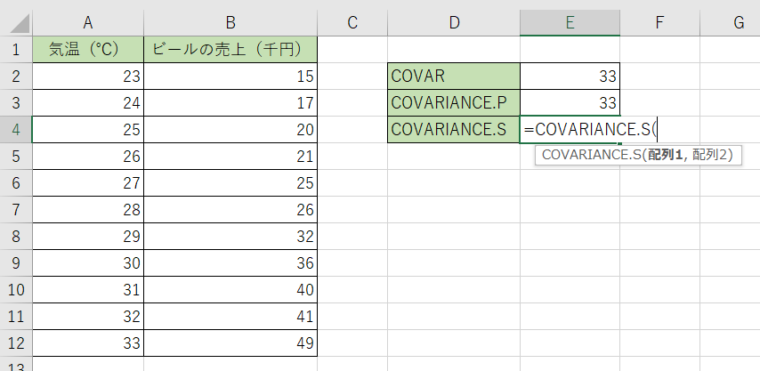
2.これまでと同じで、1つ目にA列、2つ目にB列のデータを選択します。
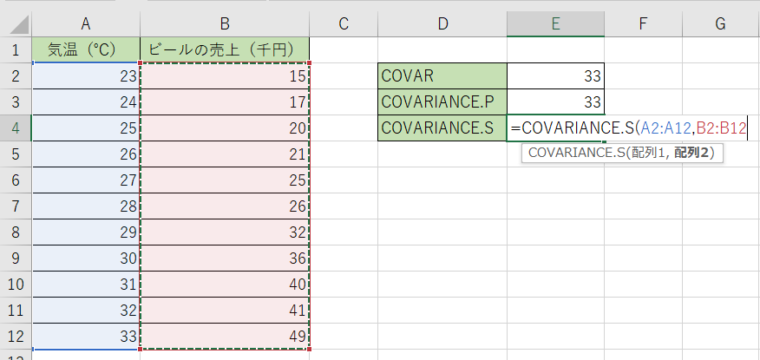
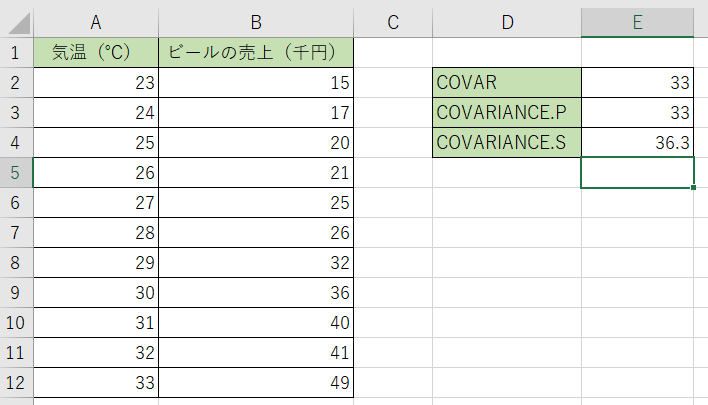
3.関数を決定すると答えが出て来ます。結果が『36.3』です
不偏共分散の計算であれば、結果の数値が大きくなりましたね。より関係性が高いという結果であると見えますね。
Excelでデータ分析!共分散を求めて数値の分析に役立てる|まとめ
今回は共分散と不偏共分散を計算する関数を3つ紹介しました。計算例で示した通り、どれを使うかによって結果の数値が変わっていきます。実際に陶芸額ではこの数値と、それぞれのデータの標準偏差から相関係数を求めて分析という感じで、さらにいろいろと求めていく事になります。
この関数の使い方と注意点をまとめると下記の様になります。
- データの集まりの関係性を表す共分散、不偏共分散を計算します。
- COVARとCOVARIANCE.Pは共分散の計算で同じ結果になります。
- COVARIANCE.Sは不偏共分散の計算になります。
エクセルにはデータの分析や解析をする時に使用出来る関数がいろいろと準備されています。今回紹介した関数についてはその中の1種類になります。データの関係性が分かる事で、今後の営業の戦略に使えたりするとよいですね。今後もいろいろな関数を紹介していくので、使いこなせるようにして行きましょう!