Excel(エクセル)で、確率分布の演算の中の二項分布に関わる計算として、確率を計算する時には、『BINOM.DIST』関数が使えるという話は覚えていますか?実際に宝くじが当たるには、何回あるいは何枚買えばいいのかという事も計算できたりするんですね。
さて、Excelの関数には使用をする時に逆を考える計算があります。今回で言えば、確率を〇%になる為の成功回数は何回かという事になる訳です。例えば
- 40回投げたコインで裏が出た確率が全部で65%になるのは何回出た時か?
- さいころを15回投げて、1が出た確率を10%にする時の成功回数は?
- 契約率が73%の人が15件商談した時に、80%の契約率にする時に何件契約結べればいいか?
という事もできますよ。3つ目の契約の話は状況分析をする時に演算できれば、より細かい分析ができるようになりそうですね。この計算をする時に使用されるのが、BINOM.INV(バイノミナル|インバース)関数になるんです。確率的にどうしたいという事が分かれば、達成する為に何をしていくのかと言った行動計画なども立てられますね。今回は、この『BINOM.INV』の使用方法や書き方を紹介します
BINOM.INV(バイノミナル|インバース)関数の動画はこちら
BINOM.DIST(バイノミナル|ディストリビューション)の説明を確認したい時はこちら
目次
『BINOM.INV関数』の書き方と使用方法
『=BINOM.INV(試行回数,成功確率,α)』
- アルファは、最終的な成功確率の数値です。0~1の間です
- 試行回数は行う回数を指定します
- 成功確率は、ベルヌーイ試行をした時の成功する確率です
二項分布の確率を演算する『BINOM.DIST』関数と逆の計算をします。確率から成功回数を求める事ができますよ。応用的な考えていけば、営業で、これまでの契約率が70%、今月は80%の契約率にしたい時に、営業件数を何件で行けばいいのかという事も考えられますね。ただし、例として書きましたが実はこの考え方で演算しようとしても、営業の場合は人が相手になる仕事ですし、契約を成功とするならば、必ず成功確率が70%でいけるとは言えないので、正確な数値にはなりません。計画を立てる上での参考数値として考えてもらうといいかもしれませんね。
バイノミナル関数で演算させる関数は、ベルヌーイ試行に置いての演算になります。ベルヌーイ試行は、1回目の試行結果が2回目に影響しない試行の事でしたね。くじ引きとかは、1人目の結果が、2人目の結果に影響があるので、正確な計算にはなりませんね。コインを投げる、カードの中から1枚選んだら元に戻してから2枚目を引く、宝くじで1等が当たるまで何年かかるか、などといった計算に使用されます。
実際に関数を使用、演算をしていきましょう!
『BINOM.INV関数』で成功回数を計算してみよう!
コインを投げるを使用して、計算をしてみましょう。引数に何を準備すればいいのか、どんな値が出て来るのかなどを覚えていきましょうね。
コインを投げた時の成功回数を出してみよう!
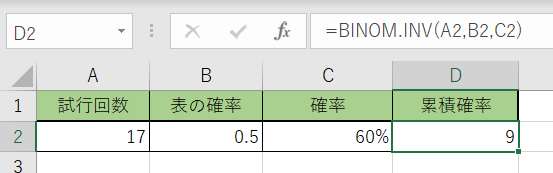
コインを17回投げた時に、1回でも表が出る確率を60%にして成功したい、という時には何回コインを投げたら良いでしょうか?投げる回数を求めてみます。

1.『D2』に、『=BINOM.INV (』を書きましょう。

2.次に引数です。1つ目にあたる引数が『試行回数』となり、引数部分の2つ目に『成功確率』、最後の引数として3つ目に『α』で最終的な確率の基準値を書きます。今回は『60%』となる訳ですね。

3.関数を決定すると、数値が出されます。今回は「9」ですね。
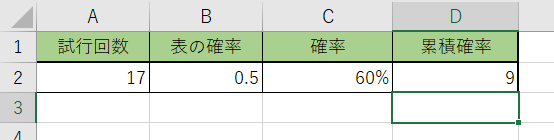
コインを15回投げた時に60%の確率で表を出す場合、『9』回投げれば良いという事ですね。
指定した値の確率になる成功回数をエクセルで計算しよう!『まとめ』
二項分布の確率を演算をできる関数のBINOM.INV(バイノミナル、インバース)関数が使用された計算については理解は深められましたでしょうか?使用時の引数さえ間違わなければ、あとは指定していくだけなので簡単にできる様になりますよ。
この関数について改めて、まとめてみると
- 二項分布の確率分布の演算で、確率から回数を計算する
- 指定する成功確率の数値と、『α(アルファ)』の数値で指定できるのは、0~1の間
という所になりますね。
二項分布の確率の演算では、『BINOM〇〇』と言う様に、バイノミナルから始まる関数になります。全部で4種類ですね。『BINOM.DIST』と『BINOMDIST』はエクセルのバージョンの違いによって使用される、使用されないという話で、計算方法は同じ関数ですね。ですので、バイノミナルの関数は実質3種類となります。『BINOM.INV』は『BINOM.DIST』の逆関数と言っても良い演算内容になっていますね。セットで覚えておきましょう。また、どんな確率を演算したいのかによって他の関数と使い分けができる様にしておくと、計算の幅が広がりますよ。ぜひ参考にしてみて下さいね。