二項分布の確率や累積分布の確率をExcel(エクセル)で計算したい時は、『BINOM.DIST』(バイノミナル・ディストリビューション)関数を使ってみましょう。この関数を使う事で、二項分布の確率と累積確率も計算する事が出来ます。
二項分布の確率というのは、例えば
- さいころを20回投げて、5が5回出る確率
- コインを5回投げて、表が3回出る確率
という内容がありますね。二項分布で確率を計算出来る条件としては、コインを投げる時の様に、1回目の結果が2回目の結果に影響を与えないという事ですね。ちなみにこれをベルヌーイ試行と言いますよ。こういった確率を計算出来るのが、『BINOM.DIST』関数になっているんですね。エクセルには、『BINOMDIST』という関数もあります。どちらも同じ確率を計算する為の関数ですので、どちらを使っても計算出来ます。『BINOM.DIST』の方が新しい関数なので、こちらを使う事が多いですね。そしてこの関数で、累積確率の計算も出来ます。今回は、関数の使い方、累積分布の計算をするにはどうしたらよいかなど説明しますね。
BINOM.DIST(バイノミナル・ディストリビューション)関数の動画はこちら
目次
『BINOM.DIST関数』『BINOMDIST関数』の使い方
『=BINOM.DIST(成功数,試行回数,成功確率,関数形式)』
『=BINOMDIST(成功数,試行回数,成功確率,関数形式)』
- 指定する引数は、どちらの関数も同じです。
- 関数形式には、『TRUE』あるいは『FALSE』を指定します。
- 『FALSE』で二項分布の確率、『TRUE』で累積確率を計算出来ます。
コインを10回投げて、3回表が出る確率であれば、試行回数が『10』成功数が『3』確率が『0.5』という事になります。関数形式を空欄にした場合は『FALSE』の指定になります。累積確率は、成功数に指定した数より少ない回数も含めてという考え方になります。『3回以下の回数表が出る』という事ですね。
実用例も踏まえて、使い方を覚えていきましょう!
二項分布の計算『BINOM.DIST』を活用してみよう
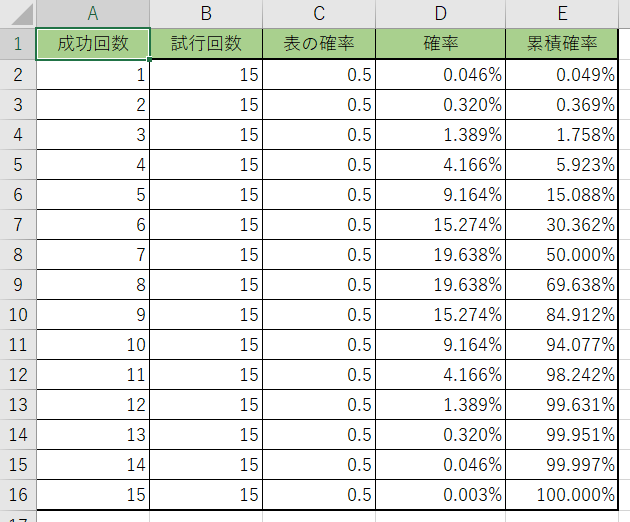
実際に、二項分布の確率と累積確率を計算してみましょう。今回はコインを15回投げて、決めた回数だけ表が出る確率を計算してみましょう!表には、試行回数を『15』、成功回数を『1~15』成功確率の『0.5』を入力してあります。
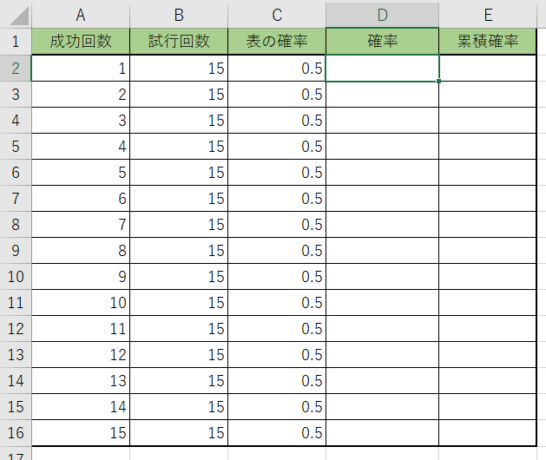
二項分布の確率を求めてみる
まずは、決めた回数ぴったりの結果が出て来る二項分布についての確率の計算をしてみましょう!
1.確率の結果を出す所に、『=BINOM.DIST(』を入力します。
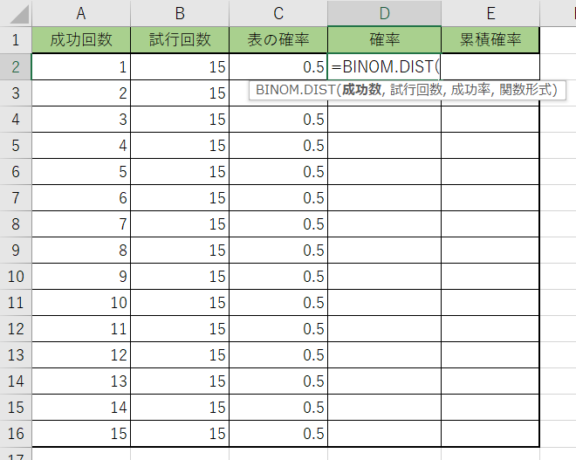
2.引数の選択では、1つ目が成功回数、2つ目に試行回数、3つ目に成功確率を選択します。
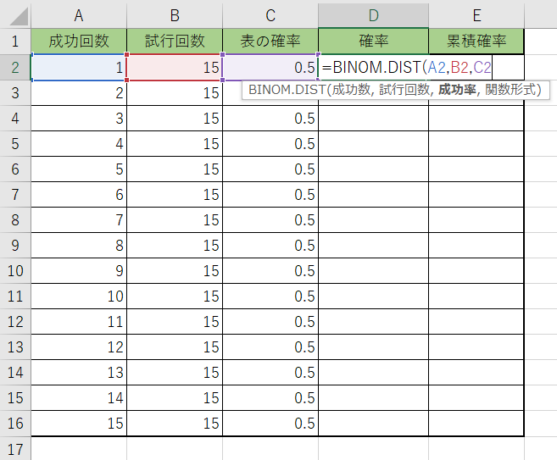
3.今回はぴったりその回数の結果になる確率なので、関数形式には『FALSE』を書きます。
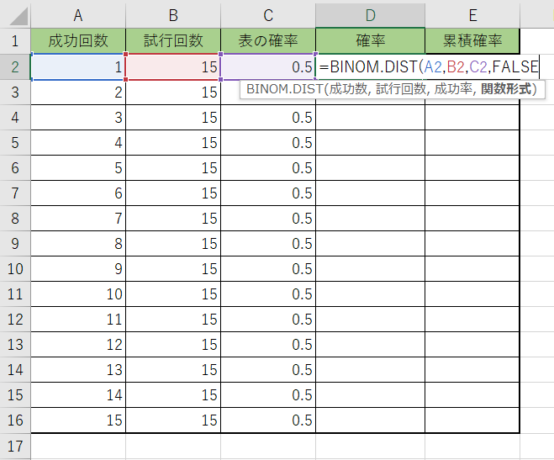
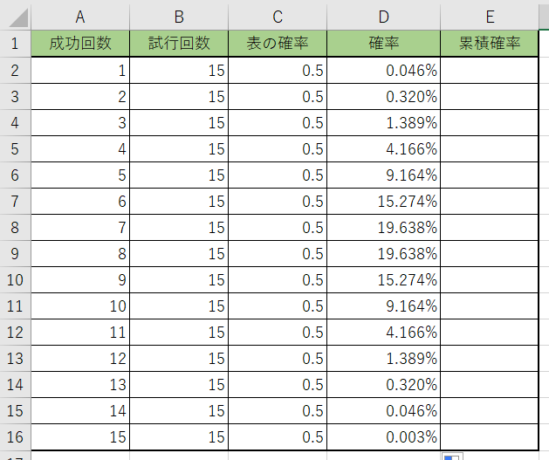
確率が計算出来ましたね。オートフィルを使って表を埋めてみましょう!
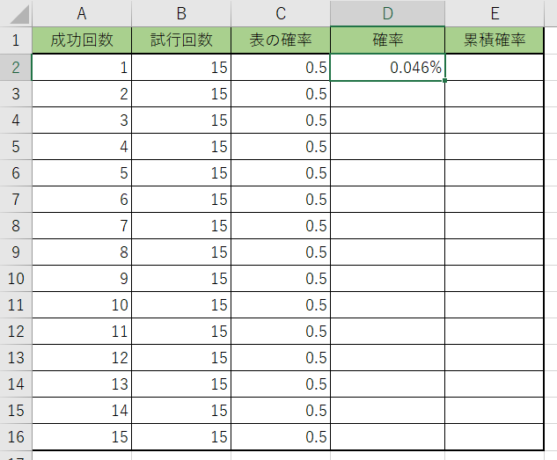
それぞれの回数での確率が求められました。
成功回数以上になる累積確率を計算してみよう
次に、累積確率を計算してみましょう。成功回数以上の回数が出て来る確率という考え方でしたね。やってみましょう!
1. 累積確率を計算する所に『=BINOM.DIST(』を入力します。
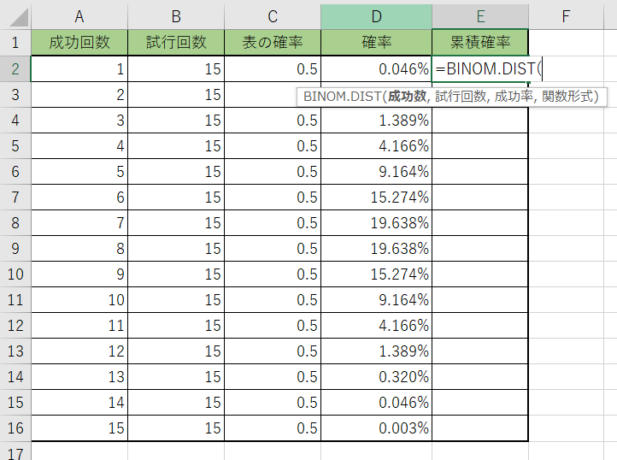
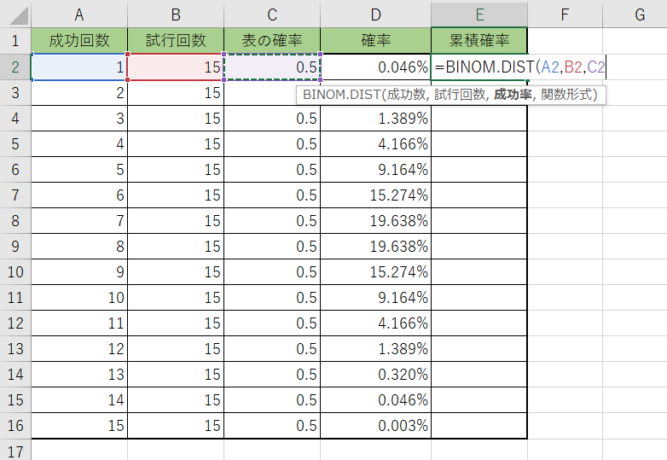
2. 引数を二項分布の計算と同じように選択していきます。
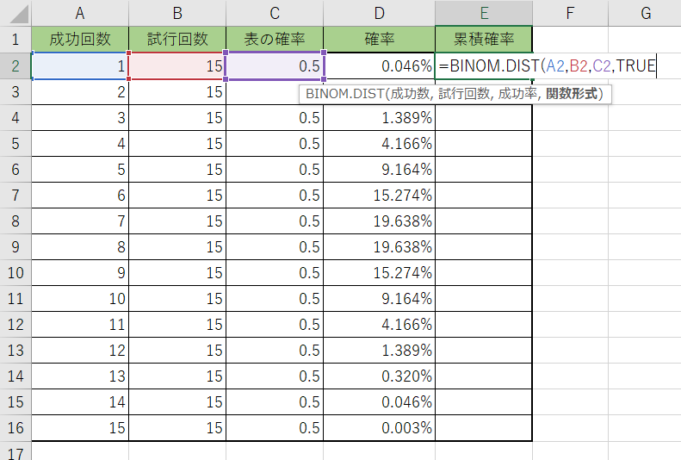
3. 関数形式の引数の所を『TRUE』を指定しましょう!
計算出来ましたね。1回以上は表が出る確率ですね。
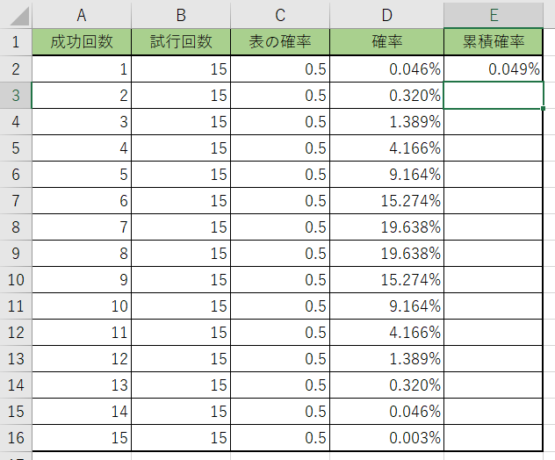
オートフィルをして、表を全て埋めましょう。
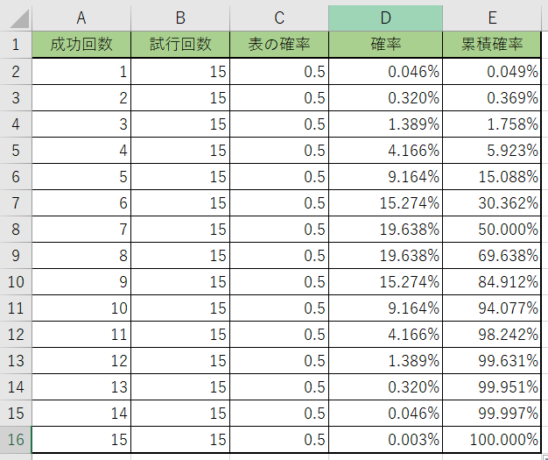
この場合、『1回以下の回数』というのに『0回』というのも含まれるので、先ほどの答えより数字が大きくなっていますね。
【応用編】二項分布確率のグラフを作ってみよう
BINOM.DIST関数を使って確率を出せましたね。この確率がどのように遷移しているのか、見やすくする為にグラフを作ってみましょう!
グラフの作成では、必要になるデータを選択してグラフの種類を選べば完成です。
試行回数と確率からグラフを作ります。
1.試行回数と確率のセルを選択します。離れたセルは『CTRL』キーを押しながら選択します。
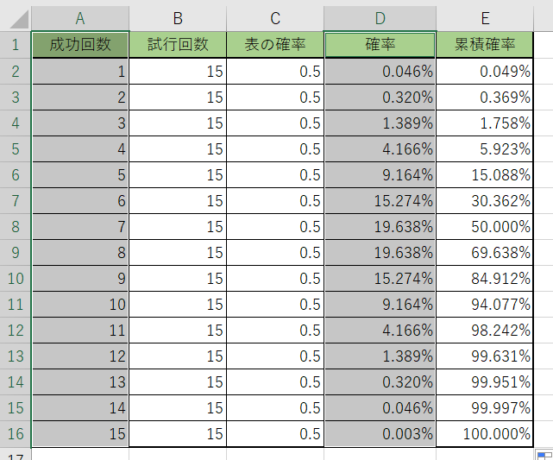
2.グラフの種類を選びます。タブは『挿入』の所にあります。今回は『集合縦棒』を選択しましょう。

3.これでグラフの完成です。
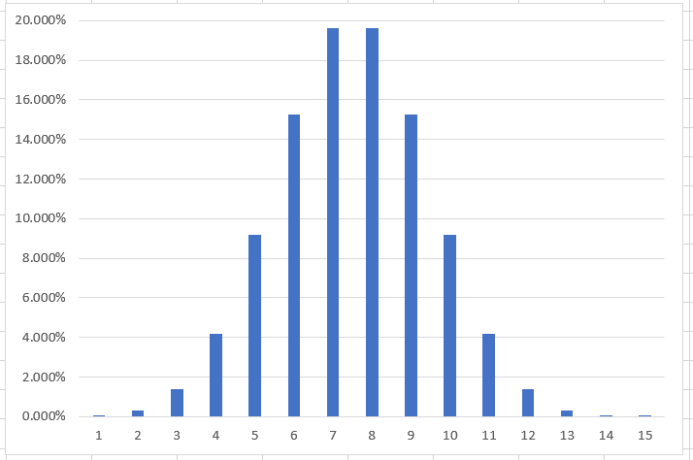
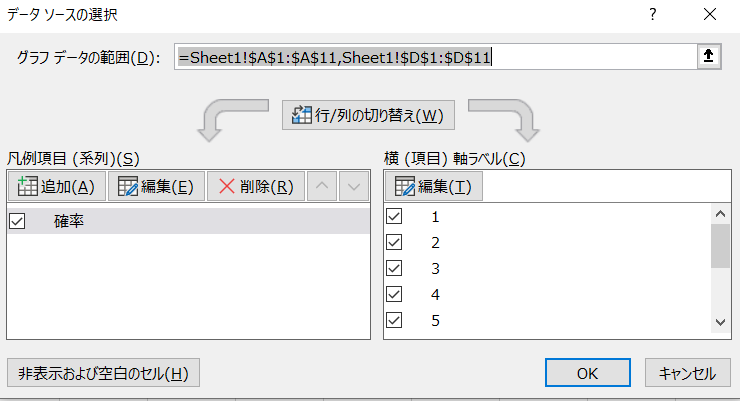
グラフが出来ないという時は、『グラブツールのデザイン』から『データの編集』をします。
凡例項目に『確率』、横軸に『試行回数』を設定しましょう。
グラフの種類については、数値の動きが分かれば、どのグラフを選んでも良いです。
『おすすめグラフ』の中から選ぶと、データに合わせたグラブの候補が出て来るので便利ですよ。
エクセルの関数で二項分布の確率、累積分布の確率を計算する!『まとめ』
関数の『BINOM.DIST』を使って、二項分布の確率と累積確率を求めるやり方について説明をしました。この関数のポイントをまとめると
- 二項分布の確率の計算が出来る
- 関数形式を『TRUE』『FALSE』の指定で計算内容が変わる
- 『TRUE』の指定で、累積の確率を計算出来る
確率を計算する内容に関わってくる関数はたくさんあります。確率の計算が出来ないという時は、選んでいる関数を間違えている可能性もあります。BINOM.DISTを使える計算は、ベルヌーイ試行をする時の話になります。ですので、福引で当たりを引く確率の様に、1回引いたら、2回目は分母の個数が変わってしまう状況の確率では使えません。こういう見極めが大事になる訳ですね。
確率に関わる他の物も今後いろいろ説明していきますので参考にしてみて下さい。