二項分布の確率を出す為のExcel(エクセル)の関数には、いくつか種類があります。その中の一つのBINOM.DIST.RANGE(バイノミナル・ディストリビューション・レンジ)関数を使ってみましょう!二項分布の計算に役立つ関数になっているので使いこなせるといいですよね。その前に二項分布の確率ってどういう物でしたでしょうか?例えば
- 50回さいころを振って、3が30回出る確率
- 20回コインを投げた時に、20回表が出る確率
- 13枚のトランプから1枚引く事を10回やった時に、11以上の数を引いた回数が8回以上の確率
と言った事が挙げられますね。二項分布で大事なのは、ベルヌーイ試行と言われる、一回目に行った行動が2回目の行動に影響を与えない試行で無いといけないという事でした。例の3番目については、トランプを1枚引いたら、それを戻してから、2回目の行動をしないとベルヌーイ試行になりませんよ。
さて、二項分布の確率の計算で、BINOM.DIST関数の説明を以前にしましたね。実はこの関数では、3番目の例の計算が出来ません。成功数の指定が1つしか出来ないからですね。範囲を指定して確率を出したい時にはBINOM.DIST.RANGE関数を使うんですね。。これをどのように使っていくのか、関数の書き方と活用方法を紹介していきます。
BINOM.DIST.RANGE(バイノミナル・ディストリビューション・レンジ)関数の動画はこちら
目次
『BINOM.DIST.RANGE関数』の書き方・使い方
『=BINOM.DIST.RANGE(試行回数,成功確率,成功数1.成功数2)』
- 成功回数が、『成功数1』から『成功数2』の間になる確率を計算します。
- 『成功数2』は省略も可能です。
- 『成功数2』を省略した場合は、BINOM.DIST関数と同じ計算になります。
『BINOM.DIST.RANGE』の引数を見ると分かる様に、成功数に『5回から10回の間』という様に、範囲を持たせて計算する事が出来ます。先ほどの3番目の例であれば、回数か8回以上になるので、引数の『成功数1』が『8』『成功数2』が『10』となればいい訳ですね。
BINOM.DIST関数とは引数の順番が違っているのと、累積確率を計算する為の『関数形式』という物はありませんので注意が必要ですね。考え方としてはBINOM.DIST.RANGE(バイノミナル・ディストリビューション・レンジ)関数は累積確率を計算する関数になるからですね。
実際に引数の指定パターンを変えて、計算をしていきましょう!
『BINOM.DIST.RANGE関数』を使える様にしよう!
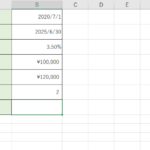
パターンに合わせて、確率の計算をやってみましょう。最初の例で書いたトランプの例でやってみます。表には、『試行回数』『成功確率』『成功数1』『成功数2』を入力しておきました。これらを使ってみます。
成功数に範囲を持たせて二項分布の確率を求めてみる
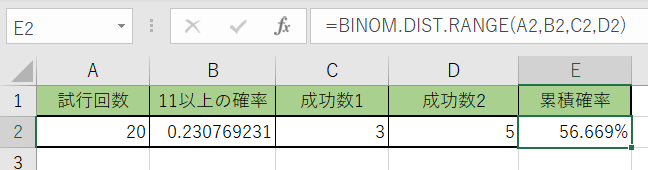
成功数に範囲を与えて、確率の計算をしてみます。今回は『20回試行』で『11以上の数』が『3回から5回』でる確率を計算します。『成功確率』は『3/13』になるので、その数字を入れておきます。

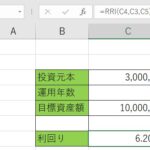
1.『E2』に、『=BINOM.DIST.RANGE(』を書きます。

2.引数を指定していきます。1つ目が『試行回数』、2つ目に『成功確率』、3つ目に『成功数1』、4つ目に『成功数2』の所を選んでくださいね。

3.これで完成となりました。計算結果を表示してみて下さいね。

成功数に範囲を持たせて計算する時には、このようにBINOM.DIST.RANGE関数の方を使いましょう!
2つの値の範囲で成功する二項分布の確率をエクセルで計算しよう!『まとめ』
二項分布の確率計算を出来る関数のBINOM.DIST.RANGE(バイノミナル・ディストリビューション・レンジ)関数を使って、成功数が複数の範囲となる確率の計算、応用で累積確率の計算をしてみました。この関数についてまとめると下記になります。
- 『2回から5回』と言った範囲を持った成功数の確率を出せる
- 引数の『成功数1』と『成功数2』の値の指定で、累積確率も出せる
成功数の範囲を指定するかしないかで使い方が変わり、範囲を指定するならBBINOM.DIST.RANGE関数で、範囲を指定しないならBINOM.DIST関数という使い方になりますね。『BINOM.DIST.RANGE』の関数での計算というのは、累積確率を計算している事になるので、『X回以下』になる確率という内容にも対応出来ます。『BINOM.DIST』関数と引数の数は同じなので、この場合はどちらの関数を使ってもいいです。使い易い方を選んで使っていって下さい。二項分布の確率を計算する関数にはもう一つあり、『BINOM.INV』(バイノミナル・インバース)関数というのがあります。厳密には確率を求める計算という訳ではありませんが、『BINOM.DIST.RANGE関数』と合わせて使い分けられる様に覚えておきたい所です。別途紹介しますので参考にしてくださいね。