Excel(エクセル)でガンマ分布の確率は『GAMMA.DIST』・『GAMMADIST』・『GAMMA.INV』・『GAMMAINV』で計算する事が出来ます。それぞれ『ガンマディストリビューション(GAMMA.DIST・GAMMADIST)』関数と『ガンマインバース(GAMMA.INV・GAMMAINV)』関数と言います。それぞれ同じ読み方で、『.』がついているか、ドット無しなのかで関数が2つに分かれている感じですね。これらはExcelのバージョンが新しくなった時に、新しく関数が出来ました。『.』がついているのが新しい関数になります。
今回のガンマ分布は待ち行列を計算する時などで使われたりしますね。1時間に300人の閲覧があるホームページを5000人に見てもらうのにかかる時間の確率とか、10分間に5人来るラーメン屋さんに100人来るのに何分かかるかとかガンマ分布でやってみたりします。
関数の操作のコツを掴んで、待ち行列の計算をして行きましょう!
【GAMMA.DIST】【GAMMADIST】【GAMMA.INV】【GAMMAINV】関数の説明動画はこちら↓↓
目次
【GAMMA.DIST】【GAMMADIST】でガンマ分布の確率を計算してみよう!
待ち行列の計算でも使えるガンマ分布の関数を使ってみましょう。この『GAMMADIST』と『GAMMA.DIST』を活用する際には引数の指定の仕方が大事になります。どんな引数が必要で、何を求める事が出来るのか、関数に違いはあるのかなど、理解して行きましょう!
【GAMMA.DIST】【GAMMADIST】の違いはどんな所かな?
ガンマ分布の計算には『GAMMA.DIST』・『GAMMADIST』がありますが、この2つはエクセルのバージョンの違いで関数が新しく出来たという事で、実は違いはありません。
これから使って行くのであれば新しい方の、『GAMMA.DIST』の方を使う事をおススメします。
関数を活用する為の引数をチェック!
『GAMMA.DIST』関数と『GAMMADIST』についてどのような引数になるのか確認をしてみよう。
関数式:『=GAMMADIST(x、α、β、関数形式)』
関数式:『=GAMMA.DIST(x、α、β、関数形式)』
- ガンマ分布の確率を計算します
- 関数形式では『TRUE』か『FALSE』を指定します。
- 『TRUE』の場合は累積分布関数、『FALSE』の場合は確率質量関数になります。
1分間にβ人来るお店にx分でα人集まる確率がいくつかを計算します。
『FALSE』の場合は確率密度を求めるので、どの時間が集まる確率が高いのかを求められます。
『TRUE』の場合は累積分布確率になりますので、この時間までで集まる確率というのが分かります。
ガンマ分布を使って待ち行列の計算をやってみよう
関数によりガンマ分布の計算をやってみますが、『GAMMA.DIST』関数と『GAMMADIST』は同じなので、新しい方を活用して、計算してみましょう。
1分間に5人来るラーメン屋さんに100人集まる時間別の確率を出してみます。
表を準備しました。内容としてはA列が求めたい時間別、B列が目標の人数、C列が1分間に集まる人数になります。
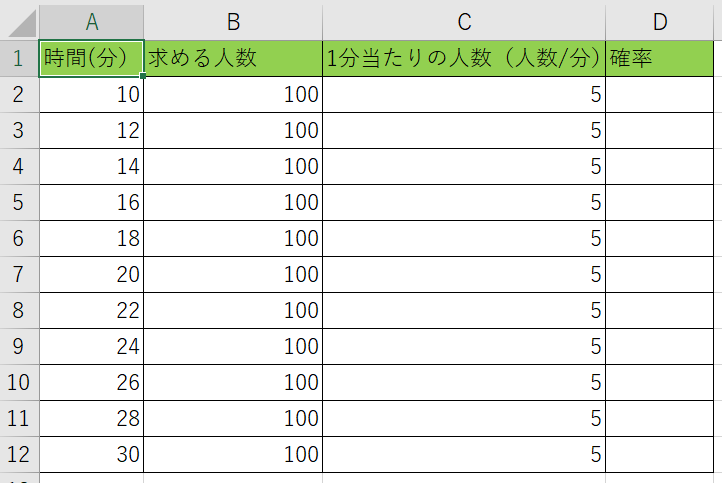
・関数形式TRUEの場合
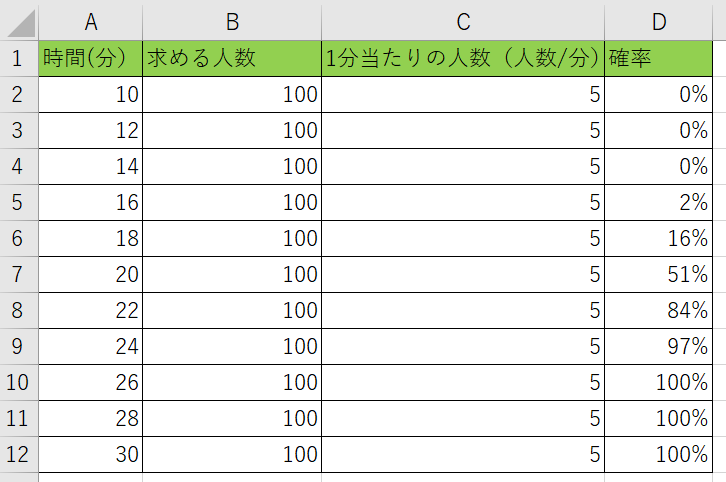
D列に『=GAMMA.DIST(A2、B2、1/C2、TRUE)』と書き込みましょう。
注意点としてはC列の人数は『1/C2』の様に逆数にしておくことですね。
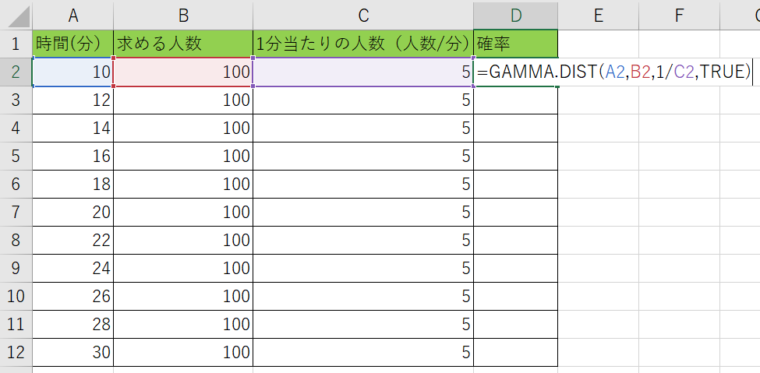
表を埋めてみると、どの時間以降で100人集まる確率が高いのかが分かりますね。
・関数形式FALSEの場合
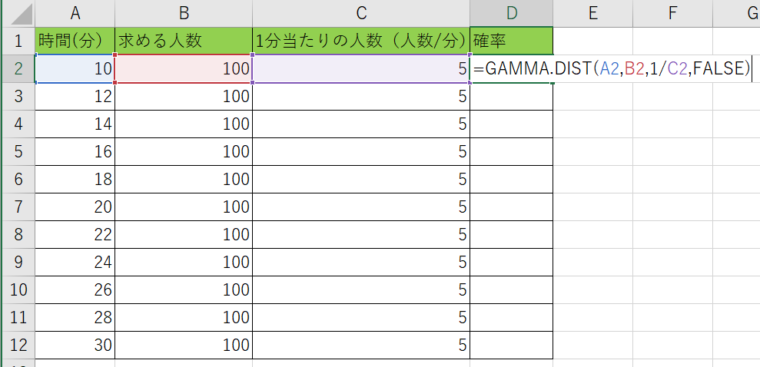
D列に『=GAMMA.DIST(A2、B2、1/C2、FALSE)』と書き込みましょう。
同様に注意点としてはC列の人数は『1/C2』の様に逆数にしておくことですね。
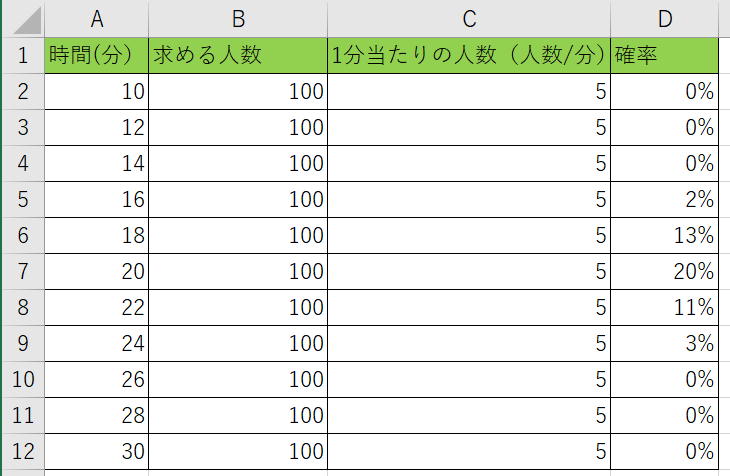
どの時間で100人集まるのかの確率が出ています。
【GAMMA.INV】【GAMMAINV】でガンマ分布の確率から待ち時間を考えてみよう!
今度はガンマ分布の確率を求める逆関数を使ってみよう。もう2つの『GAMMAINV』と『GAMMA.INV』を活用します。これを活用する事により何が求められるのかの内容を掴んで行きましょう!
【GAMMA.INV】【GAMMAINV】の違いはどんな所かな?
ガンマ分布の確率の逆関数には『GAMMA.INV』・『GAMMAINV』がありますが、この2つについてもエクセルのバージョンの違いで関数が新しく出来た物なので同じ内容になります。
これに関してもこれから使って行くのであれば新しい方の、『GAMMA.INV』の方を使う事をおススメします。
関数を活用する為の引数をチェック!
『GAMMA.INV』関数と『GAMMAINV』についてどのような引数になるのか確認をしてみよう。
関数式:『=GAMMAINV(確率、α、β)』
関数式:『=GAMMA.INV(確率、α、β)』
- ガンマ分布の確率から待ち時間の計算が出来ます。
- 指定した確率で目的の人数に達する時間が分かります
1分間にβ人来るお店に指定した確率の時にα人集まる時間がいくつかを計算します。
50%の確率で目標が達成できる時間が何分かという感じですねぇ
ガンマ分布の逆関数、待ち時間の計算をやってみよう!
関数によりガンマ分布の確率からの時間をやってみますが、『GAMMA.INV』関数と『GAMMAINV』は同じ結果となる計算なので、新しい方を活用して計算してみましょう。
1分間に5人来るラーメン屋さんに100人集まる確率別の時間を出してみます。
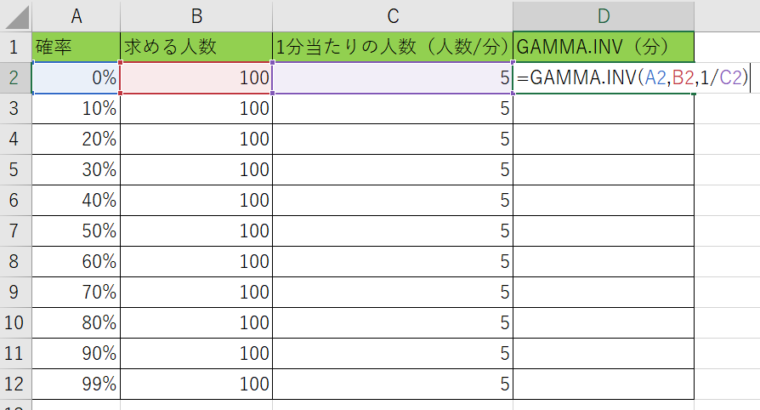
表を準備しました。内容としてはA列には基準となる確率、B列が目標の人数、C列が1分間に集まる人数になります。
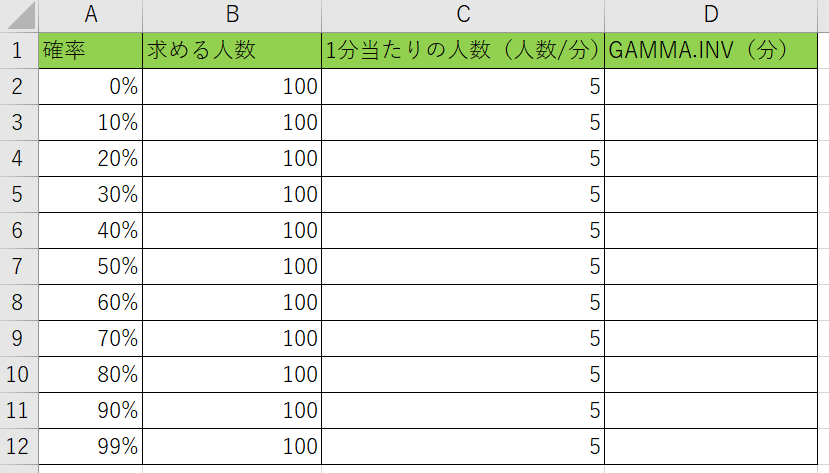
D列に『=GAMMA.INV(A2、B2、1/C2)』と書き込みましょう。
注意点としてはC列の人数は『1/C2』の様に逆数にしておくことですね。
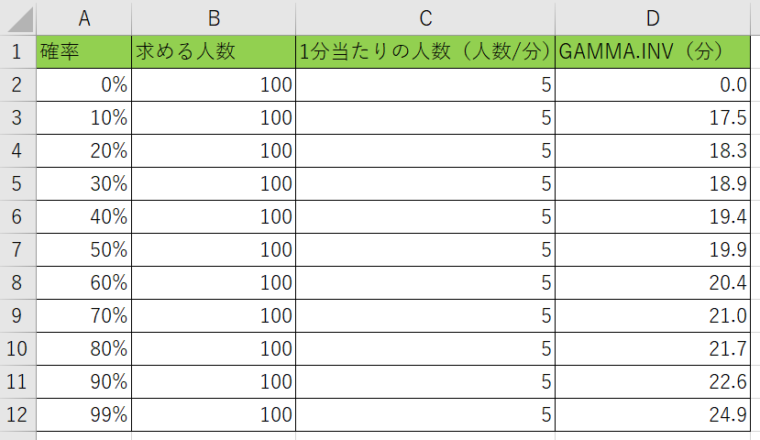
表を埋めてみると、それぞれの確率別の時間が分かりますね。
Excelで待ち行列の計算!ガンマ分布の確率を求める!【GAMMA.DIST】【GAMMADIST】【GAMMA.INV】【GAMMAINV】|【まとめ】
Excel(エクセル)で『GAMMA.DIST』・『GAMMADIST』・『GAMMA.INV』・『GAMMAINV』を活用した方法について紹介しました。関数で求められるのがガンマ分布という事になるので、待ち行列に関わる部分で計算をしています。
『GAMMA.DIST』・『GAMMADIST』に関しては行列で時間別に目標人数が集まる確率を求める事が可能であり、『GAMMA.INV』・『GAMMAINV』は指定した確率で目標人数に達する時間を出す事が可能となっている関数でしたね。
今回はラーメン屋さんでやってみましたが、この時間が分かるお店では今後の対策を考えたり、ホームページの閲覧人数から待ち時間を考えたりすると、環境の変更を考えたりする基準に出来たりする訳ですね。
分かる事によって分析が出来る事もありますので使い分けて活用して行きましょう!