Excelで利用できるPOISSON.DIST(ポアソン・ディストリビューション)関数とPOISSON(ポアソン)関数をお伝えいたします。
POISSON.DIST関数
ポアソン分布は、一定時間の中で起こりうる事柄を数値として表します。
何だか難しいお話になってしまいましたが、ポアソン分布とは、科学データのほぼほぼ正規分布に従うと考えてよいといえますが、分布においてそのデータの数が多い場合でかつある地点での交通量の発生確率のように発生しにくい何らかの条件を考える時に、ポアソン分布に近くなると考えられています。
何らかの条件のお起こりえる確率が解っているとき、データの中から何個かのデータを取り出して目的の条件が何回お起こるかの確率を求める時に使います。
見てみたほうが解りやすいかもですね!
書式は、=POISSON.DIST(事象の数, 事象の平均, 関数形式)となります。
事象の数には、 目的の事象が起こる回数を選択します。
事象の平均には、事象が平均して起こる回数を選択します。
関数形式には、 カンマ後、表示される FALSE(確率質量関数)の値を求める場合は選択し、TRUE(累積分布関数)の値を求める場合は選択します。
かっこ()の中の引数は以上となります。
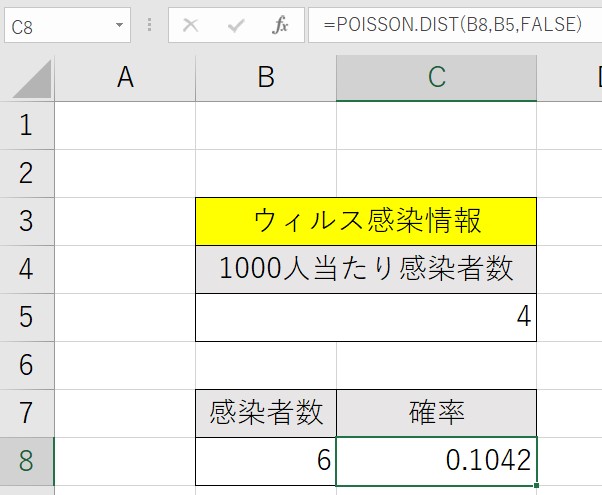
例1:コロナウィスに1000人中、平均して4人が感染しているとして6人になる確率を出してみます。
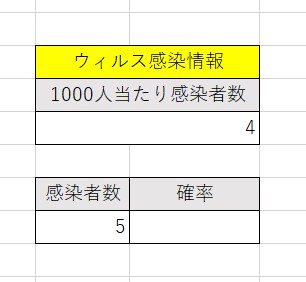
C8のセルに、書式は次の通りでしたね!=POISSON.DIST(事象の数, 事象の平均, 関数形式)
=POISSON.DIST(B8,B5,FALSE)と入力します。結果は。
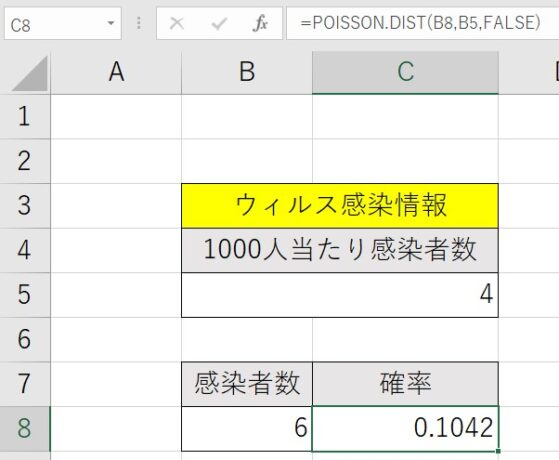
6人感染する確率は「0.1042」となりました。
例2:道路のある地点での交通事故の発生確率のように発生しにくい何らかの条件を考える時に、ポアソン分布に近くなると考えられています。
架空のお話ですが、ある地点の度重なる交通事故の発生回数は12か月で18回起きているとします。
次に1か月の間に度重なる交通事故が4回起こる確率はいくつになるのか求めていきましょう?
まずは平均の発生確率を出します。1ヶ月に今まで事故が起きている確率は18回/12ヶ月になります。
計算方法は1ヶ月×(18÷12)で1.5になります。 平均の確率は1.5となります。そこで下記の表を作成します。
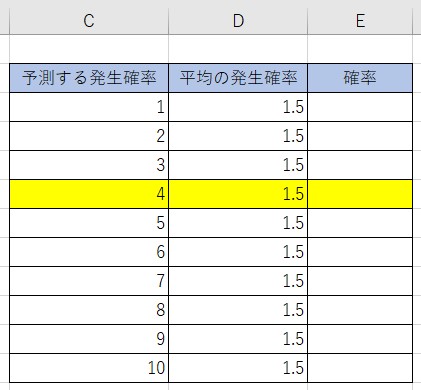
E3に、=POISSON.DIST(C3,D3,FALSE)と入力します。FALSEは、今回は予測する発生確率を出すので確率質量関数のFALSEになります。
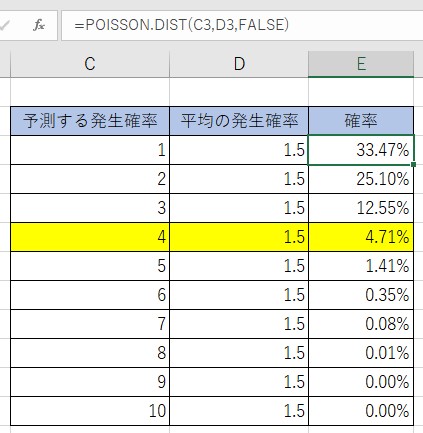
結果は「4.71%」の確率で4回事故が発生することになります。これは、何らかの手を打たないと危険な割合と考えることができますね!
POISSON関数
先にご紹介した、POISSON.DIST関数と以前のバージョンで使われていた関数になります。Office2010以上のバージョンであれば利用する事ができます。
Microsoftの解説では
POISSON関数は、精度の良いその使い方をより適切に表す名前を持つ、POISSON.DIST関数に置き換えられました。
POISSON関数は利用可能なのですが、Excelの新しいバージョンでは利用できなくなる可能性があるので、
今後はPOISSON.DIST関数を使用することをお勧めします。
との事です。確かにPOISSON関数の所に黄色の!マークが付いてますよね。
より精度が高くなるとの事なのでPOISSON.DIST関数を使いましょう!
POISSON.DIST関数とPOISSON関数のまとめです。
たまにしか起こらないような条件が大量に計測した結果がポアソン分布に従う例は極めて多く見られるとの事で、統計や科学でとても役に立つ関数ということが解ります。
POISSON.DIST関数、POISSON関数もどちらとも同じですがより精度が高くなった関数がPOISSON.DIST関数になります。
関数には良くありますが、新しい関数を使いましょうね!
これからも、もっと便利な関数をソフトキャンパスのブログで解説して参ります。