今回ご紹介する関数は、標準正規分布の密度関数の値を返す【PHI】(ファイ)関数の使い方についてご紹介いたします。標準正規分布の密度を調べるときに使われる関数なのですが、分析を行う関数はどの部分からアプローチをするかで様々な方法があります。その数ある中から今回の関数をご紹介して参ります。知っている方も知らない方も、今後の参考にぜひご覧ください!動画も参考にぜひ挑戦してみてください!
標準正規分とは?
標準正規分布とはどのようなものかと言いますと、例えばテストの点数などで、平均点の人数が一番多く、平均点から離れていくと人数が減っていく山のような形の分布の事を言います。下記の図形のように、中央に山があり左右対称の形をしているのが正規分布です。
また、正規分布の特徴は、平均から離れるほど確率分布が小さくなっていきます。こういった計算を行うには、専門的な計算式が必要になりますが、数式を覚えるにはなかなか大変なため、こうした関数を活用して頂く事で、効率よく求めることができるようになります。
統計関連の関数の種類はとても多いのですが、必要な関数を効率よく覚えることで業務もスピードアップしていくと思いますので、積極的に活用していきましょう!もし、周りで計算に困っている方がいた場合は、習得した関数を教えて差し上げてくださいね。
【PHI】(ファイ)関数の使い方
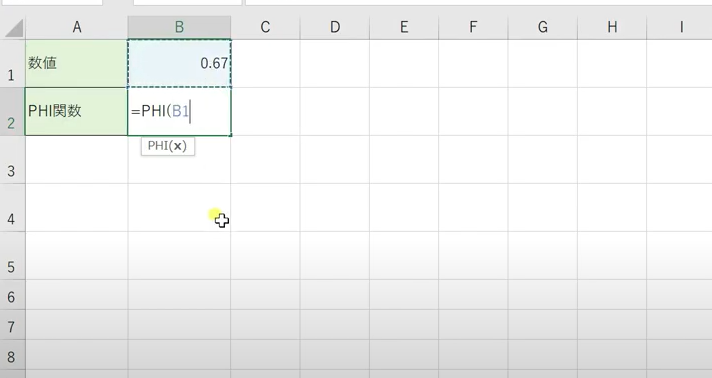
入力の仕方は
=PHI(値)
の順番で入力していきます。
値には標準正規分布の確率密度関数に代入する値を指定します。
密度を調べるための関数になります。
密度関数から、分散とかも求められたりしますね。
まとめ
今回は統計系の関数から、正規分布の確率密度関数をご紹介いたしました。これまでにも、多くの関数を紹介して参りました。種類が多いが上に、どのような時にどの関数を使用すればいいのか若干悩んでしまうこともありますが、正しく覚えることで今後に役立てていきましょう。こうした処理が手早くできるようになれば、普段のお仕事が今以上に効率よく動く事間違いない!という事ですね。
他の種類と言えば、標準正規分に対する関数には分散を求めたり、標準偏差を求めたり、尖度や歪度を求めたりする関数がありましたね。こうした関数の種類も、このブログ&動画アップをしていますので、一つでも多く覚えたい!という方は、検索して頂きぜひ網羅してみてください!関数を覚えるのは大変ですが、一度覚えると関数の便利さに後戻りができなくなりますよ!