Excel(エクセル)には三角関数がたくさんありましたね。三角関数に関係してくる物として、双曲線関数を求める関数もあります。「ハイパボリック・〇〇」「ハイパーボリック・〇〇」と言われる関数です。曲線を計算する時に使われる関数ですね。ざっくりと言うと自然界にある曲線を求める時に使ったりする関数です。
ちなみにこれらの計算は例えば、
- 電線などのぶら下がりの曲線を計算する
- 曲線のグラフの作成
- 微分や積分の計算をする
など、かなり専門的な内容の計算になりますね。ハイパボリック・〇〇と言う公式についての説明は、専門学校でも少ししか出てこなかったりする、特殊な公式になりますね。計算式すら聞いた事が無いという人も多いかもしれませんね。
この関数は少し複雑な計算が必要になりますが、Excelを使用すると簡単に数値を求める事が出来ます。簡単にハイパボリックの関数の説明と、双曲線関数の中でCSCH(ハイパボリック・コセカント)関数を使って計算の仕方をやってみます。計算の参考になるといいなぁと思います。
CSCH(ハイパボリック・コセカント)関数の説明動画はこちらから!↓↓
目次
CSCH(ハイパボリック・コセカント)関数の使用方法
『=CSCH(数値X)』
- 双曲線関数と言われる関数の1つです。
- CSCH関数は、ハイパボリック・コセカントを計算する関数です。
- SINH(ハイパボリック・サイン)の逆数になります。
- 数値Xに入る数値は「0」以外になります。
双曲線関数は三角関数と同じ性質を持っています。『SIN』の逆数が『COSEC・CSC』だったように、『SINH』の逆数が『COSECH・CSCH』になる訳ですね。この関数は、公式の性質上、数値Xが「0」だった場合、「0」の割り算になってしまう為、エラーになります。
CSCH(ハイパボリック・コセカント)ってどんな物?
双曲線関数は、三角関数から派生して出来上がった物です。どのようにして双曲線関数になったのかは、『オイラーの公式』などで調べてみると分かります。今回は細かい説明は省きます。
三角関数から派生して出来上がった公式になるので、双曲線関数の性質は、三角関数と似ています。だからSINやCOSというのも出て来る訳ですね。そして、双曲線なので、三角形は直接的に関係ないっていう事になっております。今回はCSCH関数についてですが、他についてはまた別に紹介したいと思います。
双曲線関数【CSCH】の式はどんな物?
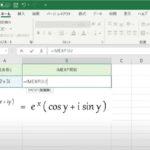
CSCH(ハイパボリック・コセカント)関数は、SINH(ハイパボリック・サイン)の逆数になります。それぞれの計算式は、次の様になります。
| 関数 | 公式 |
|---|---|
| SINH(ハイパボリック・サイン) | (e^x – e^-x)/2 |
| CSCH(ハイパボリック・コセカント) | 2/(e^x – e^-x) |
※『e』は『ネーピア数』と言われ、『約2.718』という値です
公式を比べて見ると分母と分子が逆になっている事が分かりますね。ハイパボリック・コセカントの公式の性質上、Xの値が「0」の時、分母が「0」となる為、計算する事が出来ません。
双曲線関数【CSCH】のグラフの形を表すと?
ご存知の方もいらっしゃると思いますが、なぜ双曲線関数と言われるかというと、この数式のグラフが双曲線になっているからですね。グラフで表すと以下の様な感じになります。
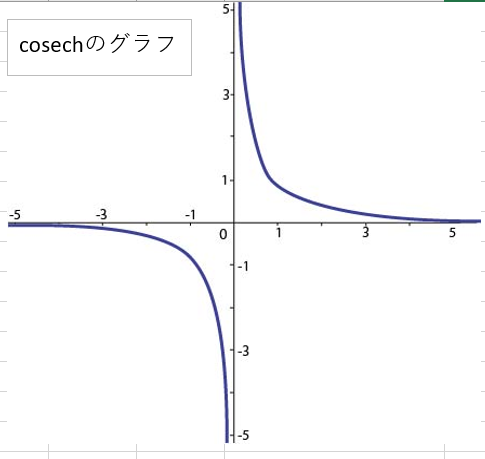
グラフを見て分かる様に、CSCHの特徴は、数値Xが「-∞」か「∞」に行けば行くほど「0」に近づいて行きます。そしてXがマイナスの数値から「0」に近づいていくと「―∞」、プラスの数値から「0」に近づくと「∞」になっていく性質があります。
Excelでこの関数のグラフを作成する場合は、Xの値を細かく変えながら数値を出して行き、それらの数値から『散布図』というフラフの種類で作成すると求められます。『0.000001』ずつという様に、かなり細かくXの数値を変えていくとより正確なグラフになりますよ。
CSCH関数を使って、数値を計算してみよう!
ハイパボリック・コセカントの公式は難しく見えますが、関数を使用しての計算は簡単に出来るようになっています。便利ですね。実際に計算をしてみましょう。
『X=1』の時のCSCHの計算
実際に関数を使って計算してみましょう。シンプルな数値として「1」の場合の数値を計算してみましょう。
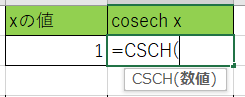
1.CSCH(ハイパボリック・コセカント)の結果を表示させるセルに、『=CSCH(』と書き込みます。
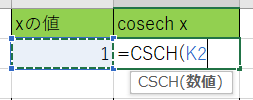
2.引数には「X」の値を入力したセルを選択します。

3.Enterで関数を確定させましょう!これで値が計算出来ましたね。
簡単に計算できるのが分かりますね。
いろいろな数値で計算するとどんな結果になる?
CSCH関数の使い方は上記で説明した通りです。後はXをいろいろな数値に変えて、どの様な値が出るか確認をしましょう。
いくつか値を入力して計算した結果は以下の通りになります。
| xの値 | cosech x |
|---|---|
| 1 | 0.850918128 |
| 0.000001 | 1000000 |
| -0.000001 | -1000000 |
| -200 | -2.76779E-87 |
| 0 | #DIV/0! |
数値が小さくなれば、計算結果が大きくなっていて、数値が大きくなれば計算結果が「0」に近く泣ているのが分かりますね。ちなみに「-200」の時は、「-2.76779×10^(-87)(10の―87乗)」というかなり小さい数値です。「0」の時は計算出来ないのでエラーになりましたね。
エクセルの双曲線関数!CSCH関数を使ってみよう!【まとめ】
Excel(エクセル)で双曲線関数のCSCH関数を使って、ハイパボリック・コサインの計算をしてみました。関数の特徴について確認すると
- SINHの逆数を計算する関数です。
- 引数にはXに入る値を指定します。
- Xが「0」の時は計算不能でエラーになります。
Excelで計算が出来ると簡単に数値を求められますし、グラフの作成も出来る様になります。数値をいろいろ変えながら試してみて下さいね。双曲線関数は、三角関数と同じ数の公式があります。SINH(ハイパボリック・サイン)やCOSH(ハイパボリック・コサイン)、呼び方が長い公式だとACOTH(ハイパボリック・アーク・コタンジェント)というのもありますね。なかなか聞く事は少ないかもしれません。エクセルにはこれらの関数が全て準備されています。計算に困ったと思ったら使用してみるのも良いですよ。何かの参考にしてくださいね。