Excelで使うチャート・スクリプト関数で、NORMINV関数・NORM.INV関数・NORM.S.INV関数・NORMSINV関数をお伝えいたします!
NORMINV関数
難しいお話になりますが、正規分布関数の累積の確立から元の値を算出してくれる関数になります。
標準偏差:データの、平均値からのばらつき具合を表し評価したり判断する目印となるもの。
正規分布:雨粒の大きさの分布とか人の身長や体重の分布、左右対称の折れ線グラフで中心を平均とした左右対称になだらかに下がっているカーブという感じです。
累積分布:たとえばサイコロを投げた時の出る目の確立の事になります。3が何%とか6が何%などの事になります。
注: NORMINV関数は別の名前に置き換えられました。NORMINV関数は利用する事は出来ますが、Excelのバージョンでは利用できなくなる可能性があるため、今後は新しい関数を使用することをお勧めいたします。
新しいExcelのバージョンを使うようになると、これからご説明するNORM.INV関数を利用するようにして下さいね。
書式は、=NORMINV(確率,平均,標準偏差)を利用していきます。。
書式には、 次の()内には引数があります。
確率には、 必ず指定します。 正規分布における確率を選択します。
平均には、 必ず指定します。 対象となる分布の平均を選択します。
標準偏差には、必ず指定します。 対象となる分布の標準偏差を選択します。
平均と標準偏差で表される累積確率から、対応する元の値を求めることが出来ます。
たとえば、全員のテスト結果をもとにして、上位から30%以上に入る為には何点取取らないといけないのかを求めることができます。
例1:上位10%に入るためには何点取れば上位1割以上に入ることが出来るかを調べてみましょう。
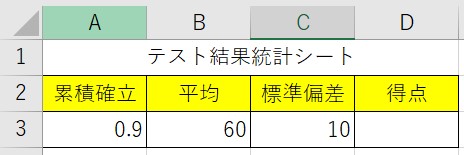
下記の表を参照してくださいね!
「D3」に、=NORMINV(B5,C5,D5)と入力します。結果は「72.8」点とれば上位1割以内に入ることが出来ると言う事になります。

ポイント
いずれの引数も、省略すると0が指定されたものとみなされます。
例を見てみると、上位10%は、下位から90%ということなので、1-0.1でセルB5には0.9が入力されています。
なお、例1はテストの平均が60点、標準偏差が10点の分布になっている場合の参考例になります。
NORM.INV関数
正規分布する乱数を発生させる
正規分布する乱数とは?
「乱数」というのはバラバラに数値を抽出することです。
「正規分布」とはデータが平均値の付近に集まっている分布を指します。
書式は、=NORM.INV(確率,平均,標準偏差)になります。
例1:先程のNORMINV関数のExcelの表をもう一度見てくださいね。

それは「E5」の=NORMINV(B5,C5,D5)をNORMINV関数ではなく数式バーのNORMINVを選択して消します。Nと入力すると出てきますのでNORM.INVに変更してみましょう。

結果は一緒なんです。NORMINV関数もNORM.INV関数も名前は少し違いますが同じ関数になります。先ほどご説明したようにNORM.INV関数はExcel2010からの新しい関数名表示に替わりました。
精度が増しているので新しいNORM.INV関数を利用するようにしましょう!
NORM.S.INV関数
標準正規分布の累積分布関数の逆関数(x軸とy軸を逆に見ることになります)の値を返します。この分布は、平均が0で標準偏差が1である正規分布に対応します。
書式は、=NORM.S.INV(確率)を使っていきます。
()内の引数の確率ですが、必ず指定します。正規分布における確率のデータを選択します。
正規分布における確率を0以上1以下の数値で選択する。
例1:入力されている値から標準正規分布の累積分布関数の値を求めてみます。
こちらも先ほどの解説にあったように、サイコロを投げた時の出る目の確立の事になります。3が何%とか6が何%などの事になります。
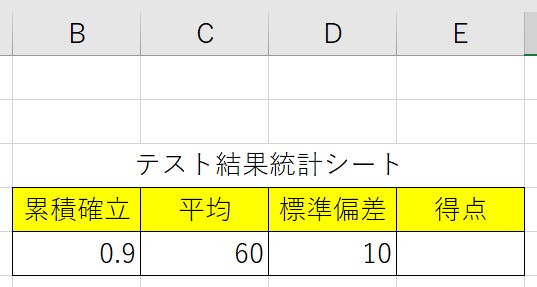
下のExcelの表を見てみましょう。「C4」に、=NORM.S.INV(C3)と入力します。
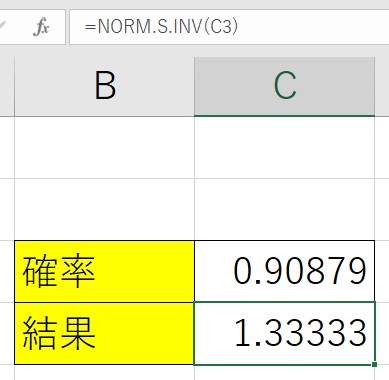
正規分とは先ほど説明したように雨粒の大きさの分布とか人の身長や体重の分布、左右対称の折れ線グラフで中心を平均とした左右対称になだらかに下がっているカーブという感じです。
例えば、人の身長や体重を始めとした非常に多くのデータはこの正規分布に従うことになります。
さらにデータでは、中心極限定理と呼ばれる統計学における重要な定理が当てはまるんですね。
この定理は、母集団が正規分布に従わない場合でも標本平均は正規分布に従うという理屈であり、この理屈のおかげでデータがとても扱いやすくなります。
こんな理由から、正規分布は統計学においては非常に重要なのものなんですね?
NORMSINV関数
標準正規分布の累積分布関数の逆関数(x軸とy軸を逆に見ることになります)の値を返します。この分布は、平均が0で標準偏差が1である正規分布に対応します。
※新しいバージョンのExcelは新機能の方がその機能をより精密に表しているため、新しいNORM.S.INV関数を使用することをあ勧めします。以前のバージョンのExcelでも引き続き使用することは出来ます。
新しいバージョンのExcelを使用している場合はNORM.S.INV関数を使用することをあ勧め致します。
書式は、=NORMSINV(確率)を利用します。
()内の引数の確率は、必ず指定します。正規分布における確率のデータを選択します。
正規分布における確率を0以上1以下の数値で指定する。
例1:のExcelをもう一度使いますので確認しましょう。

先ほどNORM.S.INV関数を使って出しましたが、関数だけをNORMSINV関数に変更してみましょう。「C4」に、=NORMSINV(C3)と入力します。
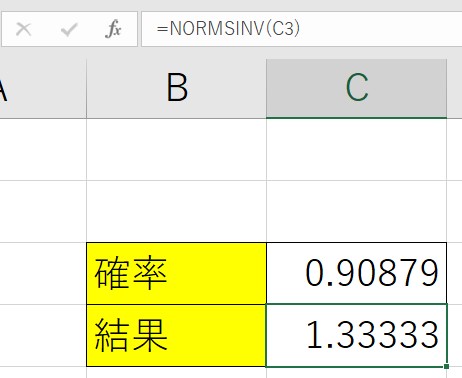
NORM.S.INV関数のドットの入らない関数になります。Excel2010以降はNORM.S.INV関数に変更になりました。
NORMINV関数・NORM.INV関数・NORM.S.INV関数・NORMSINV関数のまとめ
どの関数も.が付くかつかないかで、NORMINV関数・NORM.INV関数もNORM.S.INV関数・NORMSINV関数も新旧で同じ関数になります。
標準正規分布の累積分布関数の逆関数(x軸とy軸を逆に見ることになります)の値を返します。この分布は、平均が0で標準偏差が1である正規分布に対応します。
※NORMSINV関数、2010以降のExcelは新機能の方がその機能をより精密に表しているため、新しいNORM.S.INV関数を使用することをあ勧めします。以前のバージョンのExcelでも引き続き使用することは出来ます。
新しいバージョンのExcelを使用している場合は新機能を使用することをあ勧め致します。
使って頂きたい関数は先程ご紹介いたしましたNORM.S.INV関数になります。
集団が正規分布に従わない場合でも標本平均は正規分布に従うという理屈であり、この理屈のおかげでデータがとても扱いやすくなります。
上記の理由から、正規分布は統計学において非常に重要なのものである事が解っております。
使い方を覚えてExcelがこれまで以上にもっと便利になります、是非覚えてくださいね!
これからも引き続き関数ブログをアップして参りますので、気になる関数があったらまずはソフトキャンパスのブログを確認してみてくださいね!