目次
IMCOT関数(イマジナリー・コタンジェント エンジニアリング)
指定された複素数の余接を返してくれます。 たとえば、x+yi、x+yj形式で複素数を指定するとcot(x+yi)が返されます。
複素数?とは数直線上に表せる数(実数)と表せない数(虚数)を合わせた数の概念になります。
2 乗して−1になる数を「虚数単位 i」と考えます。虚数単位 i とは、
i2乗=−1またはi=√−1を満たす数であり、iを含む数を虚数と言います。
どんな実数も2乗すれば必ず0以上になるので、iを含む数は確かに実数ではないことになります。
では、複素数の定義を確認してみましょう。実数A,Bと先程の虚数単位iを使って「A+Bi」と表される数を複素数と言います。
実数でない数なんて必要あるの?かと思うかもしれません。
でも、現代の物理学のすべての分野の発展に複素数は貢献しているんだそうです。
光、音、電磁波、交流電流などの「波動」の分野で必要な数になるんですね!
電気や電波に囲まれた私達の国は、複素数に支えられていると言っても過言ではないんです。
虚数で人間の現実世界が成り立っている?何だか不思議で神秘的ですよね。
余接とは、三角関数のサイン(正弦),コサイン(余弦),タンジェント(正接),コタンジェント(余接),セカント(正割),コセカント(余割)と呼びます。
余接はコタンジェントの事ですね!
書式は、=IMCOT(複素数)になります。
「1+i」のコタンジェントを求めてみましょう。
A2のセルに=IMCOT(“1+i”)と入力します。結果は「0.217621561854403-0.868014142895925i」となりました。

イマジナリー・コタンジェント エンジニアリング関数の名前通り、エンジニアリングや高度な数学で専門的な用途で使うことを想定した関数になります。
・単位や基数の変換・複素数の計算・ベッセル関数等を行うことが出来るんですね。
IMCSC関数(イマジナリー・コセカント エンジニアリング)
今度は、文字列 “x+yi” または “x+yj” の形式で指定された複素数の余割を返します。
余割なので、コセカントを返します。サインの逆数になります。
書式は、=CSC(数値)になります。
以下のデータを参考にして見て下さいね!

C3のセルには、=IMCSC(0.213)と入力してください。C4のセルには、=IMCSC(“2-2i”)と入力します。
結果が表示されました。サイン関数の逆関数で表示されましたね!
IMCSCH関数(ハイパーボリック・イマジナリー・コセカント エンジニアリング)
今までと同様に、文字列 “x+yi” または “x+yj” の形式で指定された複素数の双曲線余割を返してくれます。
双曲線余割とは、同じ数値に対する双曲線正弦(ハイパーボリック・サイン)の値のこちらもコセカントなので逆数になります。
双曲線関数になるので、確率計算の近似値を求めたりするときに使います。
書式は、=IMCSCH(数値)になります。
こちらも、以下のデータを参考にして見て下さいね!
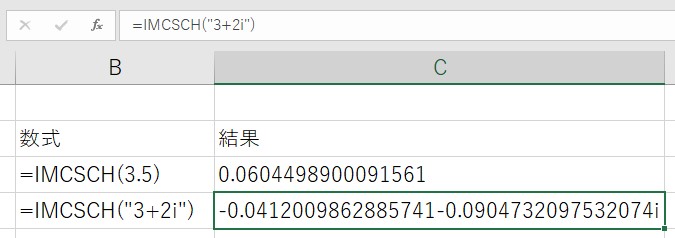
C3のセルに、=IMCSCH(3.5)と入力します。C4のセルには、=IMCSCH(“3+2i”)と入力してください!
結果が表示されたと思います。複素数の双曲線余割が返りました。
IMCOT関数・IMCSC関数・IMCSCH関数のまとめ
IMCOT関数は複素数の余接を返してくれます。
IMCSC関数は複素数の余割を返してくれます。
IMCSCH関数は、複素数の双曲線余割を返してくれます。でしたね。
エンジニア関数になるので一般では利用すことがなかなかない関数ですが、理系の方などは覚える必要がありそうですね!
CONPLEX関数を使うと、実数と虚数を指定すると複素数に変換することが出来るんです。
複素数が文字列の時には”x+yi”又は”x+yj”の文字列の場合には返してくれますが、それ以外はエラーになります。
又、複素数に論理値を返した場合もエラーになりますので注意してくださいね!!