今回の関数は、三角関数の1種で双曲線正弦を求める【SINH】(ハイパボリック・サイン)関数と、同じく三角関数の1種で数値の双曲線正接を求める【TANH】(ハイパボリック・タンジェント)関数の解説になります。この関数は曲線を計算する際に使用する関数なのですが、実は三角形とはあまり関係がない関数だったりするのですが、数値の考え方が三角関数のSINやCOSと似ているからという話もあったりします。とはいえ、双曲線関数は求めるのがとても難しいので、こうした便利な関数を使用することで、効率よく計算することができるようになるのです。通常難しい公式や計算をするものでも、関数にすることによって簡単に求めることができるものが多いです。知らずにいるよりも、一つでも多くの関数を知っていることで、作業もはかどるはずです!
ブログと一緒に動画も見て、参考にしてみてください!!
【SINH】(ハイパボリック・サイン)関数
入力の仕方は
=SINH(数値)
の順番で入力していきます。
ハイパボリック・サインの計算式は【ex-e-x/2】(2分のeのx乗 マイナスeのマイナスx乗)グラフは下記の画像のようになります。
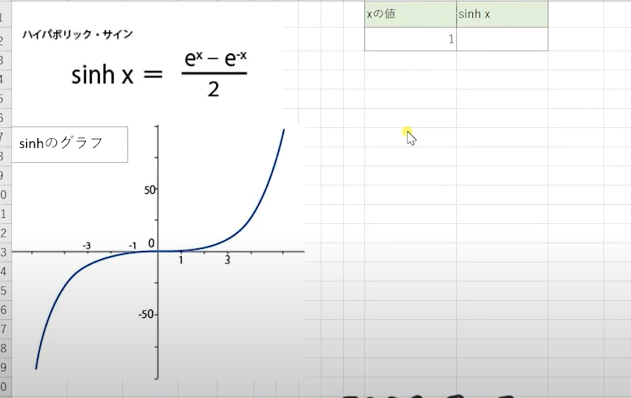
双曲線関数は、三角関数の種類分あります。種類が多くて覚えるのも大変ですが、頑張って覚えることで作業効率を上げることができると思います!
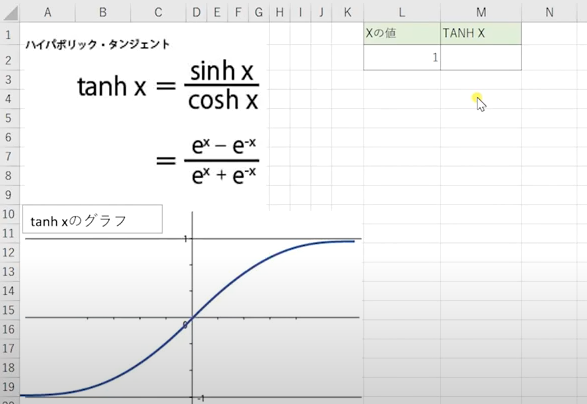
【TANH】(ハイパボリック・タンジェント)関数
入力の仕方は
=TANH(数値)
の順番で入力していきます。
双曲線は、x軸、y軸、原点に対して対象な曲線で、「平面において異なる2つの定点F,F’からの距離の差が0にならない一定の値をとる点Pの軌跡」という定義があります。
まとめ
ここまでご覧頂き有難うございます。普段は使用用途の無いという方も、積極的にいろいろな関数を使いこなせるようになって頂くととてもうれしいです!
今回の関数は三角関数という特殊な関数にはなっていますが、覚えてみると意外な使い道があるかもしれません。三角関数や公式、双曲線など理数系が苦手という方にはぜひ覚えて頂きたいです。関数はそうした覚えるにはとても大変な数式や公式を、関数を覚えることでカバーすることができるわけなので、理屈や関数の根本を理解していくのは最初は大変ですが、慣れてくれば関数を覚えることがどれだけ便利で、簡単な計算なのかという事も理解して頂けると思います!今回の関数だけではなく、他にも便利な関数は多数あります。これを機会に様々な関数に興味を持っていただけたらとてもうれしいです!
Youtube動画には400種を超える関数の紹介動画を配信しています。一気に見るのはとても大変だと思いますので、検索して興味のある関数からぜひチャレンジしてみてください!
引き続き、動画・ブログを宜しくお願い致します。