今回ご紹介する関数は、Excelでベッセル関数の値を求める関数になります。関係する関数は複数あり、今回は一挙にご紹介して参ります。【BESSELI】(ベッセル・アイ)関数、【BESSELJ】(ベッセル・ジェイ)関数、【BESSELK】(ベッセル・ケイ)関数、【BESSELY】(ベッセル・ワイ)関数の4種類をご紹介していくのですが、似ているようでそれぞれ使う用途が異なります。まず、【BESSELI】(ベッセル・アイ)関数は、第一種変形ベッセル関数の値を求める際に使用すると大変便利な関数になります。電磁波などの波の解析などを行う際に使用される関数になります。【BESSELJ】(ベッセル・ジェイ)関数は、量子力学などで使用される波紋のような波の計算で使われる関数になります。Σ計算になりますので、時間がかかりそうな計算になりますが、この関数を使用することで、便利に効率よく計算することができます。【BESSELK】(ベッセル・ケイ)関数は、第二種変形ベッセル関数を計算する際に使用される関数になります。数学や力学を知らないととても難しい関数になると思います。ですが、関数を使用すれば楽に計算し求めることが可能になります。最後に、【BESSELY】(ベッセル・ワイ)関数です。こちらも第二種ベッセル関数の計算を行いたい時に使用する関数になりますね。こうした計算には、詳細な定理などありますが、ベッセル関数で検索して頂くと量子力学などの説明が出てきますので、参考にして頂ければと思います。動画内でも解説をしておりますので、ぜひご覧ください!
目次
【BESSELI】(ベッセル・アイ)関数の入力方法について
まずは、【BESSELI】(ベッセル・アイ)関数の入力方法から確認をしていきます。
=BESSELI(数値,次数)

上記のように入力をして求めていきます。
数値は、第1種変形ベッセル関数の値を求めたい変数xを数値で指定します。
次数は、次数nを数値で指定します。負の値を指定することはできません。

こうして計算を行っていくと、電磁波の解析や振動波の計算をすることができます。第一種ベッセル関数の計算式は、上記画像のようになっています。
こちらを計算しようと思ったら、手間もかかりますし難しくてお手上げ状態になってしまうかもしれませんが、関数を使う事でこれを実現しています。
【BESSELJ】(ベッセル・ジェイ)関数の入力方法について
次に、【BESSELJ】(ベッセル・ジェイ)関数の入力方法から確認をしていきます。
=BESSELJ(数値,次数)

上記の画像のように入力を行います。
また、第一種ベッセルカンストは、円柱座標や極座標系の有限振動現象を扱うのに有効になります。例として、太鼓の振動や、ミュージックシンセサイザーの波形を解析するなどに応用して使うことができるものです。

【BESSELK】(ベッセル・ケイ)関数の入力方法について
3つ目は、【BESSELK】(ベッセル・ケイ)関数の入力方法から確認をしていきます。
=BESSELK(数値,次数)
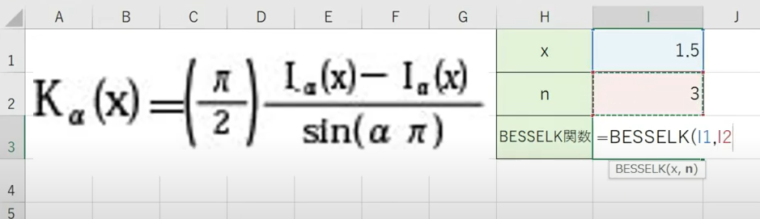
第二種変形ベッセル関数の計算結果を求めることができます。
上記の画像のような計算式が、第二種変形ベッセル関数の計算式になります。
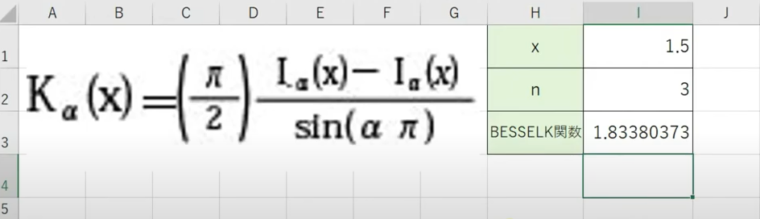
【BESSELY】(ベッセル・ワイ)関数の入力方法について
最後は、【BESSELY】(ベッセル・ワイ)関数の入力方法から確認をしていきます。
=BESSELY(数値,次数)
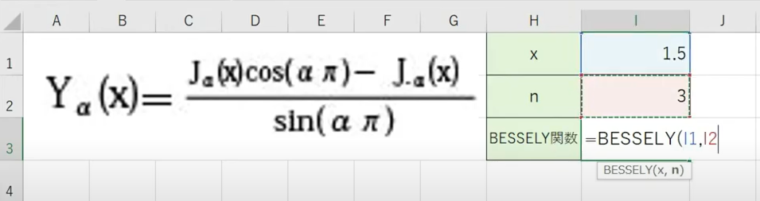

上記のように入力を行うと、第二種変形ベッセル関数の計算結果を求めることができます。
と、このように4種類の関数を一気にご紹介してきたのですが、いかがでしたでしょうか。正直、専門分野すぎて分からない・・・という方もいらっしゃると思うのですが、専門で扱っている方にとってもは、とても重要な関数だと思います。
数学や力学を学んでいないと、そもそも何のためにその関数を活用したらいいのか、逆に悩んでしまいそうなくらい、専門的な関数ではありましたが、関数に興味をお持ちの方は是非、これを機会に挑戦してみてください!詳細な定理などについては、検索をしてみて頂ければ調べることができると思いますので、こちらもぜひ挑戦してみてください。では、引き続き関数ブログと動画を宜しくお願い致します。